What Is The Derivative Of X+1/x
News Co
Apr 24, 2025 · 5 min read
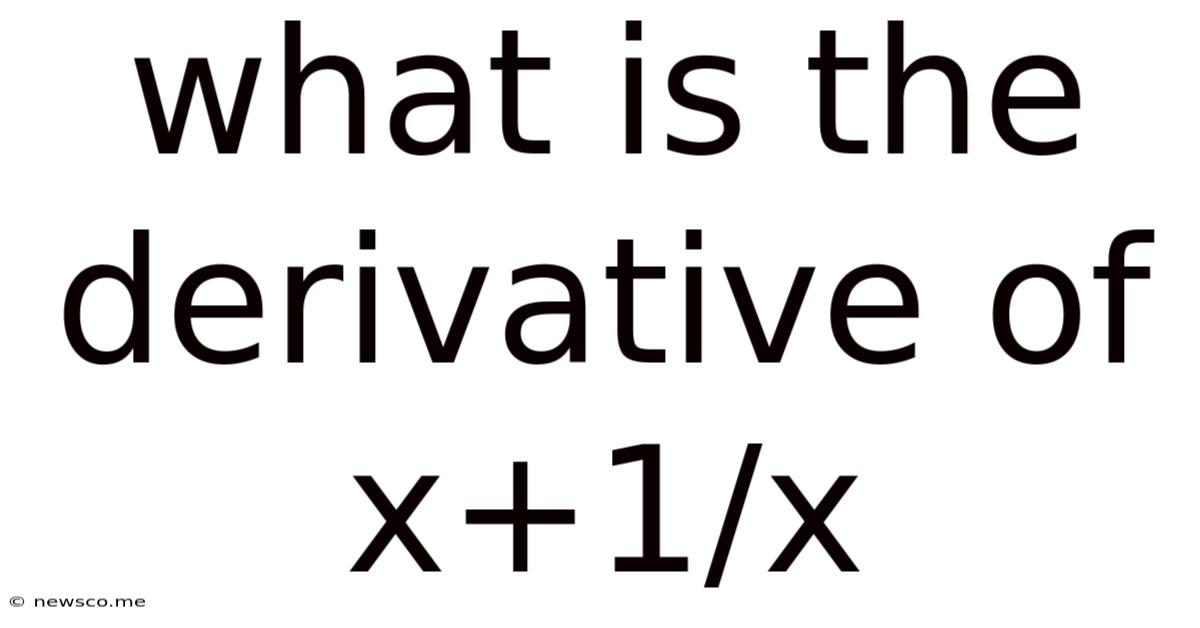
Table of Contents
What is the Derivative of x + 1/x? A Comprehensive Guide
The seemingly simple function, f(x) = x + 1/x, offers a rich opportunity to explore fundamental concepts in calculus, specifically differentiation. This comprehensive guide will not only provide the answer but delve into the why and how, equipping you with a deeper understanding of derivatives and their applications.
Understanding Derivatives: A Quick Refresher
Before diving into the specific derivative, let's establish a firm grasp on the core concept. The derivative of a function at a specific point represents the instantaneous rate of change of that function at that point. Geometrically, it's the slope of the tangent line to the curve at that point. This instantaneous rate of change is crucial for understanding various phenomena in physics, economics, and engineering.
The process of finding a derivative is called differentiation. Several rules govern differentiation, which we'll utilize to solve our problem.
Key Differentiation Rules
- Power Rule: The derivative of x<sup>n</sup> is nx<sup>n-1</sup>. This is the most fundamental rule.
- Sum/Difference Rule: The derivative of a sum (or difference) of functions is the sum (or difference) of their derivatives. d/dx [f(x) ± g(x)] = f'(x) ± g'(x).
- Constant Multiple Rule: The derivative of a constant times a function is the constant times the derivative of the function. d/dx [cf(x)] = c * f'(x).
- Reciprocal Rule: The derivative of 1/f(x) is -f'(x) / [f(x)]<sup>2</sup>. This is particularly relevant to our example.
Differentiating x + 1/x: A Step-by-Step Approach
Now, let's apply these rules to find the derivative of f(x) = x + 1/x.
-
Applying the Sum Rule: We can differentiate each term separately:
d/dx [x + 1/x] = d/dx (x) + d/dx (1/x)
-
Differentiating x: Using the power rule (x<sup>1</sup>), the derivative of x is simply 1.
d/dx (x) = 1
-
Differentiating 1/x: Here, we employ the power rule in conjunction with the constant multiple rule. Rewrite 1/x as x<sup>-1</sup>.
d/dx (1/x) = d/dx (x<sup>-1</sup>) = -1x<sup>-2</sup> = -1/x<sup>2</sup>
-
Combining the Derivatives: Adding the derivatives of both terms, we get:
d/dx [x + 1/x] = 1 + (-1/x<sup>2</sup>) = 1 - 1/x<sup>2</sup>
Therefore, the derivative of x + 1/x is 1 - 1/x<sup>2</sup>.
Understanding the Result: Implications and Interpretations
The derivative, 1 - 1/x², tells us about the slope of the tangent line to the curve y = x + 1/x at any given point x. Let's explore some key implications:
-
Asymptotic Behavior: The function f(x) = x + 1/x has a vertical asymptote at x = 0. The derivative reflects this; as x approaches 0, the term -1/x² becomes infinitely large, indicating an increasingly steep slope.
-
Critical Points: Critical points occur where the derivative is zero or undefined. Setting 1 - 1/x² = 0, we find:
1 = 1/x² x² = 1 x = ±1
These are the critical points of the function. At x = 1 and x = -1, the tangent line is horizontal (slope = 0).
-
Concavity: The second derivative reveals the concavity of the function. Let's find the second derivative:
d²/dx² [x + 1/x] = d/dx [1 - 1/x²] = d/dx [1 - x<sup>-2</sup>] = 2x<sup>-3</sup> = 2/x³
The second derivative, 2/x³, is positive when x > 0 and negative when x < 0. This indicates that the function is concave up for x > 0 and concave down for x < 0.
- Applications: Understanding the derivative of x + 1/x has applications in various fields. For instance, in physics, it could model the velocity of an object whose position is given by x + 1/x. In economics, it might represent the marginal cost or marginal revenue of a certain production function.
Alternative Approach: Using the Quotient Rule
While the power rule and sum rule sufficed, we can also demonstrate the derivative using the quotient rule. This offers an alternative perspective and reinforces the understanding of different differentiation techniques.
Recall the quotient rule: d/dx [f(x)/g(x)] = [g(x)f'(x) - f(x)g'(x)] / [g(x)]²
Let's apply it to our function, rewriting it as:
f(x) = x + 1/x = (x² + 1)/x
Here, f(x) = x² + 1 and g(x) = x. Their derivatives are:
f'(x) = 2x g'(x) = 1
Now, applying the quotient rule:
d/dx [(x² + 1)/x] = [x(2x) - (x² + 1)(1)] / x² = (2x² - x² - 1) / x² = (x² - 1) / x² = 1 - 1/x²
This confirms our previous result, demonstrating the versatility of differentiation techniques.
Expanding the Knowledge: Related Functions and Concepts
Understanding the derivative of x + 1/x forms a strong foundation for tackling more complex functions. Let's briefly explore some related concepts:
-
Derivatives of More Complex Rational Functions: The same principles can be extended to more intricate rational functions (functions that are ratios of polynomials). Mastering the quotient rule is essential for handling these.
-
Partial Derivatives (Multivariable Calculus): If x were a function of other variables, we would move into the realm of partial derivatives, where we differentiate with respect to one variable while holding others constant.
-
Applications in Optimization Problems: Finding critical points (where the derivative is zero) is fundamental in optimization problems, helping us determine maximum and minimum values of functions.
Conclusion: Mastering Differentiation
Finding the derivative of x + 1/x, while seemingly straightforward, provides a valuable exercise in applying key differentiation rules and interpreting the results. Understanding the derivative's significance – its representation of instantaneous rate of change and its use in determining critical points and concavity – empowers you to analyze and interpret functions in various contexts. This detailed exploration highlights the importance of a solid understanding of calculus fundamentals and their practical applications. Remember to practice applying these rules to a variety of functions to solidify your understanding and build confidence in your calculus skills. The more you practice, the more proficient you will become in tackling more advanced mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Derivative Of X+1/x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.