What Is The Exact Value Of Tan 30
News Co
Mar 26, 2025 · 5 min read
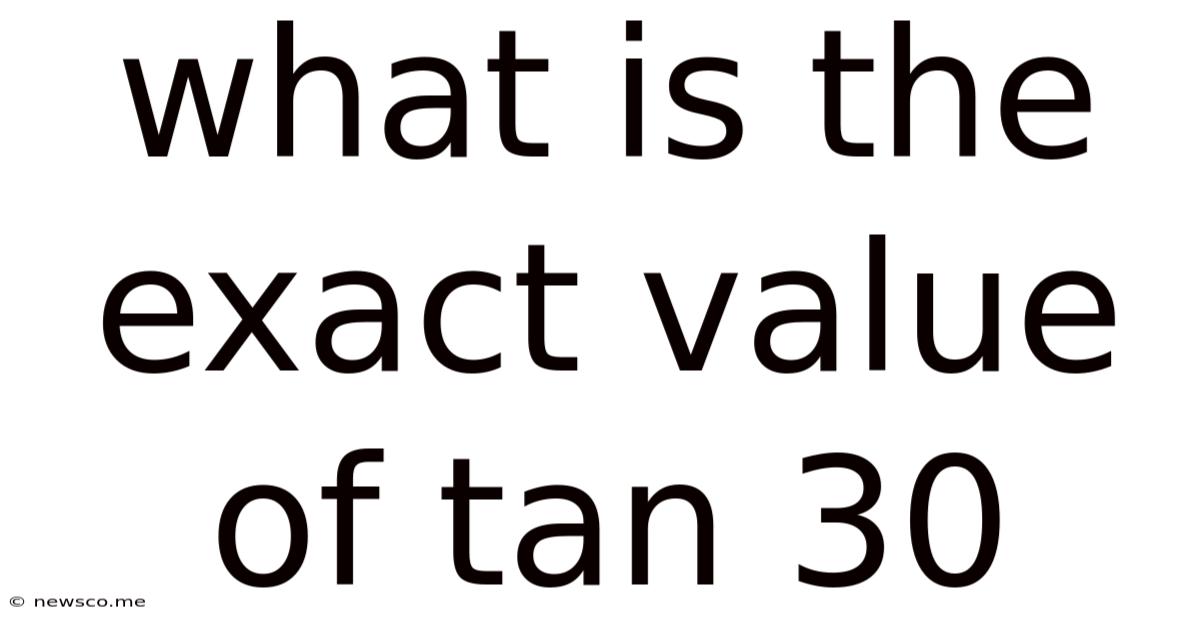
Table of Contents
What is the Exact Value of tan 30°? A Deep Dive into Trigonometry
Trigonometry, the branch of mathematics dealing with the relationships between the angles and sides of triangles, is fundamental to many fields, from architecture and engineering to physics and computer graphics. Understanding trigonometric functions like tangent is crucial. This article delves into the exact value of tan 30°, exploring its derivation, applications, and significance within the broader context of trigonometry.
Understanding the Tangent Function
Before we determine the exact value of tan 30°, let's refresh our understanding of the tangent function. In a right-angled triangle, the tangent of an acute angle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
tan θ = Opposite / Adjacent
Where:
- θ represents the angle.
- Opposite is the length of the side opposite to the angle θ.
- Adjacent is the length of the side adjacent to the angle θ (but not the hypotenuse).
This definition is crucial for understanding how we derive the exact value of tan 30°.
Deriving the Exact Value of tan 30°: The Unit Circle Approach
One of the most common ways to find the exact value of trigonometric functions is using the unit circle. The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. Points on the unit circle can be represented by their coordinates (cos θ, sin θ), where θ is the angle formed by the positive x-axis and the line connecting the origin to the point.
For a 30° angle (or π/6 radians), we can visualize a 30-60-90 triangle inscribed within the unit circle. This special triangle has sides in the ratio 1:√3:2. The hypotenuse is always 1 (the radius of the unit circle). The side opposite the 30° angle has length 1/2, and the side adjacent to the 30° angle has length √3/2.
Therefore, using the definition of the tangent function:
tan 30° = Opposite / Adjacent = (1/2) / (√3/2) = 1/√3
To rationalize the denominator (a standard practice in mathematics to avoid irrational numbers in the denominator), we multiply the numerator and denominator by √3:
tan 30° = (1/√3) * (√3/√3) = √3/3
Therefore, the exact value of tan 30° is √3/3.
Deriving the Exact Value of tan 30°: Using a 30-60-90 Triangle
Alternatively, we can directly use the properties of a 30-60-90 triangle. This special right-angled triangle has angles of 30°, 60°, and 90°. The sides are always in a specific ratio:
- Side opposite 30°: 1
- Side opposite 60°: √3
- Hypotenuse: 2
Using this triangle, we can directly calculate tan 30°:
tan 30° = Opposite / Adjacent = 1 / √3 = √3/3
This approach reinforces the result obtained using the unit circle.
Applications of tan 30°
The exact value of tan 30° has numerous applications across various fields:
1. Solving Triangles:
Knowing the exact value of tan 30° allows for precise calculations in solving right-angled triangles. If one angle and one side are known, we can use the tangent function to find the lengths of other sides.
2. Engineering and Architecture:
In construction and engineering, calculating slopes, angles of elevation, and other geometric aspects often involves the tangent function. Accurate calculations are critical for structural stability and design. For instance, determining the slope of a roof or the angle of a ramp often requires using the tangent function with angles like 30°.
3. Physics:
Many physics problems, particularly in mechanics and optics, involve the use of trigonometric functions. Calculating projectile motion, resolving forces, or determining angles of refraction often require precise knowledge of trigonometric ratios, including tan 30°.
4. Computer Graphics and Game Development:
In computer graphics and game development, precise angles and rotations are crucial for rendering realistic images and animations. The tangent function, along with other trigonometric functions, is essential for calculating rotations, transformations, and perspectives in 2D and 3D environments. Understanding the exact value of tan 30° contributes to accurate representations.
5. Navigation:
Navigation systems, whether terrestrial or celestial, rely heavily on trigonometry. Calculating distances, bearings, and positions often involve the use of trigonometric functions, including the tangent function.
Importance of Knowing the Exact Value
While calculators can approximate the value of tan 30°, knowing the exact value (√3/3) is crucial for several reasons:
- Accuracy: Calculators provide approximations, which can lead to inaccuracies in calculations, especially when dealing with complex problems requiring multiple steps. The exact value ensures precision.
- Understanding: Knowing the derivation helps understand the underlying mathematical concepts, fostering deeper learning and problem-solving abilities.
- Efficiency: Using the exact value is often more efficient than using a calculator approximation, particularly in mathematical proofs and derivations.
- Symbolic Manipulation: In advanced mathematics, working with exact values allows for symbolic manipulation and simplification of complex expressions.
Beyond tan 30°: Exploring Other Trigonometric Values
While we have focused on tan 30°, understanding other key trigonometric values is equally important. These values, often derived using similar methods involving unit circles and special triangles, form the foundation for more complex trigonometric calculations. For instance, understanding the values of sin 30°, cos 30°, sin 45°, cos 45°, tan 45°, sin 60°, cos 60°, and tan 60° provides a solid base for advanced trigonometry.
Conclusion: The Significance of tan 30° in Mathematics and Beyond
The seemingly simple value of tan 30° = √3/3 is far more significant than it initially appears. It's a cornerstone of trigonometry, enabling precise calculations in various fields. Understanding its derivation and applications highlights the power and elegance of mathematical concepts and their far-reaching consequences. From solving simple triangles to complex engineering projects, the exact value of tan 30° plays a vital role in ensuring accuracy, efficiency, and a deeper understanding of the mathematical world around us. Mastering this fundamental concept opens the door to exploring more advanced topics in mathematics and its related fields. The journey from understanding the basic definition of the tangent function to grasping the exact value of tan 30° is a testament to the beauty and utility of mathematical principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Exact Value Of Tan 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.