What Is The Factor Of 31
News Co
Apr 05, 2025 · 5 min read
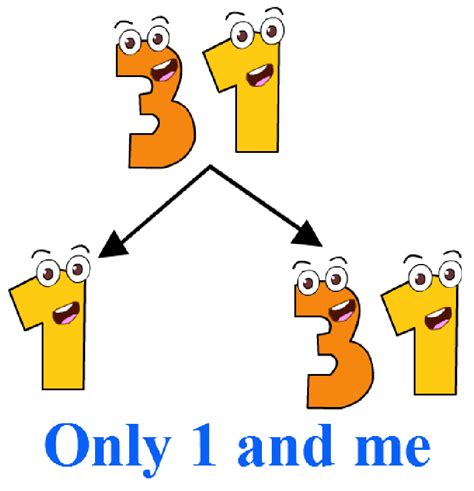
Table of Contents
What is the Factor of 31? A Deep Dive into Prime Numbers and Factorization
The question, "What is the factor of 31?" might seem deceptively simple. However, understanding the answer requires a journey into the fascinating world of number theory, specifically focusing on prime numbers and their unique properties. This article will explore not only the factors of 31 but also delve into the broader concepts of prime factorization, divisibility rules, and the significance of prime numbers in mathematics and cryptography.
Understanding Factors and Divisibility
Before we tackle the specific case of 31, let's establish a firm understanding of what constitutes a factor. A factor (or divisor) of a number is an integer that divides the number without leaving a remainder. In simpler terms, if you divide a number by a factor, the result is a whole number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. This is because 12 can be evenly divided by each of these numbers. Notice that factors always come in pairs. For instance, 2 and 6 are a pair of factors of 12 because 2 x 6 = 12. Similarly, 3 and 4 form another pair.
Divisibility rules provide shortcuts for determining whether a number is divisible by certain factors. For example:
- Divisibility by 2: A number is divisible by 2 if its last digit is an even number (0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 10: A number is divisible by 10 if its last digit is 0.
These rules can significantly speed up the process of finding factors, especially for larger numbers.
Prime Numbers: The Building Blocks of Numbers
Prime numbers play a crucial role in understanding factors. A prime number is a whole number greater than 1 that has only two distinct positive divisors: 1 and itself. This means that it cannot be factored into smaller whole numbers other than 1 and the number itself.
Examples of prime numbers include 2, 3, 5, 7, 11, 13, and so on. The sequence of prime numbers is infinite, meaning there's no largest prime number. The distribution of primes is a complex and fascinating area of mathematical research.
Numbers that are not prime are called composite numbers. Composite numbers can be expressed as the product of two or more prime numbers. This process is known as prime factorization.
Finding the Factors of 31
Now, let's address the original question: What are the factors of 31?
Applying the definition of a factor and the concept of prime numbers, we can determine that 31 is a prime number. This is because the only positive integers that divide 31 without leaving a remainder are 1 and 31 itself.
Therefore, the factors of 31 are simply 1 and 31.
The Significance of Prime Numbers
Prime numbers might seem like a niche area of mathematics, but they have far-reaching implications across various fields:
1. Cryptography: The Foundation of Secure Communication
Prime numbers form the backbone of modern cryptography, the science of secure communication. Many encryption algorithms, such as RSA (Rivest-Shamir-Adleman), rely on the difficulty of factoring extremely large numbers into their prime components. The computational power required to factor such numbers is immense, making these encryption methods highly secure.
2. Number Theory: A Cornerstone of Mathematical Research
Prime numbers are fundamental objects of study in number theory, a branch of mathematics dealing with the properties of integers. Many unsolved problems in number theory, like the Riemann Hypothesis, relate directly to the distribution and behavior of prime numbers. Understanding prime numbers is key to advancing our knowledge of number theory and its related areas.
3. Computer Science and Algorithm Design
Prime numbers are used in designing efficient algorithms for various computer science applications. For example, they are employed in hash table design, which is crucial for data structures and database management.
Beyond 31: Exploring Factorization Techniques
While finding the factors of 31 is straightforward, determining the factors of larger numbers requires more sophisticated techniques. Here are some common methods:
1. Trial Division: A Simple but Time-Consuming Approach
Trial division involves systematically testing each integer from 2 up to the square root of the number to see if it is a divisor. If a divisor is found, the number is composite; otherwise, it's prime. This method is simple to understand but becomes extremely inefficient for large numbers.
2. Sieve of Eratosthenes: An Efficient Method for Finding Primes
The Sieve of Eratosthenes is a more efficient algorithm for finding all prime numbers up to a specified integer. It works by iteratively marking the multiples of each prime number, leaving only the primes unmarked. This method is significantly faster than trial division for finding primes within a given range.
3. Factorization Algorithms for Large Numbers
For extremely large numbers, specialized factorization algorithms are necessary. These algorithms, such as the general number field sieve, are computationally intensive and are used in cryptography research and breaking encryption codes.
Conclusion: The Importance of Understanding Factors and Primes
The seemingly simple question of finding the factors of 31 leads us to a rich and complex mathematical landscape. Understanding prime numbers, factorization techniques, and their applications is crucial not just for mathematical exploration but also for various practical applications in computing and cryptography. The ability to identify prime numbers and perform factorization efficiently is a cornerstone of modern technology and security. Therefore, delving into the world of factors and primes is not just an exercise in number theory, but a journey into the fundamental building blocks of mathematics and their profound influence on our digital world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Factor Of 31 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.