What Is The Fraction Of 4/5
News Co
Apr 13, 2025 · 5 min read
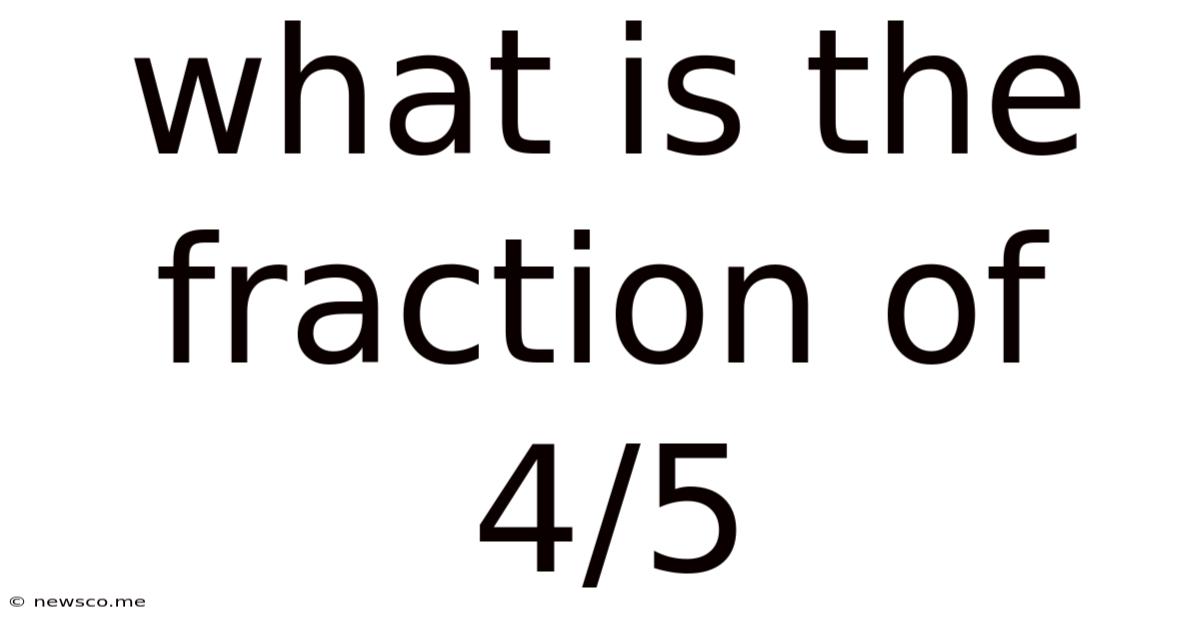
Table of Contents
What is the Fraction 4/5? A Deep Dive into Fractions, Decimals, and Percentages
The seemingly simple question, "What is the fraction 4/5?" opens a door to a broader understanding of fractions, their representation, and their applications in various contexts. This article delves into the meaning of 4/5, explores its equivalent forms (decimals and percentages), and demonstrates its use in real-world scenarios. We'll also cover related concepts to solidify your grasp of fractional arithmetic.
Understanding Fractions: The Building Blocks
Before we dissect 4/5, let's establish a solid foundation in fraction terminology. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number (in this case, 4). It indicates the number of parts you have.
- Denominator: The bottom number (in this case, 5). It indicates the total number of equal parts the whole is divided into.
Therefore, 4/5 signifies that we have 4 parts out of a total of 5 equal parts. Imagine a pizza cut into 5 slices. If you eat 4 of them, you've consumed 4/5 of the pizza.
Visualizing 4/5
Visual aids are invaluable for understanding fractions. Consider these representations of 4/5:
- A Pie Chart: A circle divided into 5 equal segments, with 4 of them shaded.
- A Bar Graph: A rectangle divided into 5 equal sections, with 4 of them colored.
- A Number Line: A line segment divided into 5 equal parts, with a marker placed at the 4th division.
These visual representations help solidify the concept that 4/5 represents a portion, less than the whole but more than 3/5.
Equivalent Fractions: Different Forms, Same Value
It's crucial to understand that 4/5 isn't the only way to express this fractional value. Equivalent fractions represent the same proportion but use different numerators and denominators. You can create an equivalent fraction by multiplying or dividing both the numerator and the denominator by the same number (excluding zero).
For example:
- Multiplying by 2: (4 x 2) / (5 x 2) = 8/10
- Multiplying by 3: (4 x 3) / (5 x 3) = 12/15
- Multiplying by 4: (4 x 4) / (5 x 4) = 16/20
All these fractions – 8/10, 12/15, 16/20, and so on – are equivalent to 4/5. They represent the same portion of the whole.
Simplifying Fractions: Finding the Lowest Terms
The fraction 4/5 is already in its simplest form. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. In this case, the GCD of 4 and 5 is 1, meaning they share no common factors other than 1.
To simplify a fraction, you find the GCD of the numerator and denominator and then divide both by that number. For example, if you had the fraction 12/18, the GCD is 6. Dividing both by 6 gives you 2/3, which is the simplest form.
Converting 4/5 to a Decimal
Fractions and decimals are two different ways to represent the same value. To convert 4/5 to a decimal, you simply divide the numerator (4) by the denominator (5):
4 ÷ 5 = 0.8
Therefore, 4/5 is equivalent to 0.8.
Converting 4/5 to a Percentage
Percentages represent a fraction out of 100. To convert 4/5 to a percentage, you can follow these steps:
- Convert to a decimal: As shown above, 4/5 = 0.8
- Multiply by 100: 0.8 x 100 = 80
- Add the percent sign: 80%
Therefore, 4/5 is equivalent to 80%.
Real-World Applications of 4/5
Understanding 4/5 has practical applications in various real-world situations:
- Cooking: A recipe might call for 4/5 of a cup of flour.
- Shopping: A store might offer a discount of 4/5 off the original price.
- Measurement: A project might require a piece of wood that is 4/5 of a meter long.
- Probability: The probability of a certain event might be expressed as 4/5.
Fractions, Decimals, and Percentages: A Unified Perspective
It's important to see the interconnectedness of fractions, decimals, and percentages. They're different ways of expressing the same proportion. Being able to convert between these forms enhances your mathematical flexibility and problem-solving skills. The ability to easily switch between these representations is crucial for tackling more complex mathematical problems and real-world applications.
Further Exploration: Operations with Fractions
Understanding 4/5 is a stepping stone to more complex fractional arithmetic. Let's briefly touch upon basic operations:
Addition and Subtraction of Fractions
To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the LCM as the denominator.
For example: 1/2 + 2/5. The LCM of 2 and 5 is 10. So, we rewrite the fractions: 5/10 + 4/10 = 9/10.
Multiplication of Fractions
Multiplying fractions is straightforward: Multiply the numerators together and the denominators together.
For example: (2/3) x (4/5) = (2 x 4) / (3 x 5) = 8/15
Division of Fractions
To divide fractions, you invert (flip) the second fraction and then multiply.
For example: (2/3) ÷ (4/5) = (2/3) x (5/4) = 10/12 = 5/6
Conclusion: Mastering Fractions, One Step at a Time
The seemingly simple fraction 4/5 provides a rich context for understanding the broader world of fractional arithmetic. By exploring its equivalent forms, visualizing its meaning, and applying it to real-world scenarios, we gain a deeper appreciation for its significance in mathematics and beyond. Understanding these fundamental concepts lays a strong foundation for tackling more advanced mathematical problems and navigating various aspects of daily life where fractions, decimals, and percentages are commonplace. Continuous practice and exploration of these concepts will solidify your understanding and enhance your problem-solving abilities. Remember that mastering fractions is a journey, not a destination, and each step you take builds upon the previous one.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Fraction Of 4/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.