What Is The Gcf Of 10 And 35
News Co
Mar 28, 2025 · 5 min read
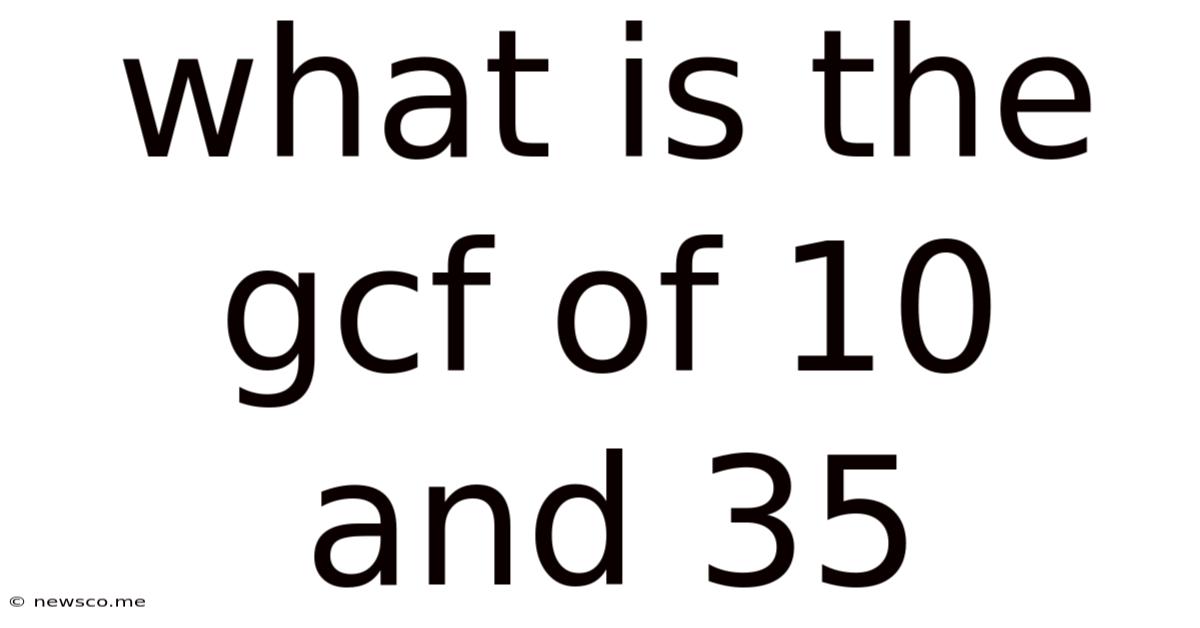
Table of Contents
What is the GCF of 10 and 35? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for solving it is crucial for a strong foundation in mathematics. This comprehensive guide will not only answer the question, "What is the GCF of 10 and 35?" but also explore various methods to determine the GCF, delve into the significance of GCFs, and provide practical applications in different mathematical contexts.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides evenly into two or more numbers without leaving a remainder. It's a fundamental concept in number theory with widespread applications in algebra, geometry, and other areas of mathematics. Finding the GCF helps simplify fractions, solve equations, and understand relationships between numbers.
Key Concepts:
- Factors: Factors are numbers that divide evenly into a given number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
- Common Factors: Common factors are numbers that are factors of two or more given numbers. For example, the common factors of 12 and 18 are 1, 2, 3, and 6.
- Greatest Common Factor: The GCF is the largest of the common factors. In the example above, the GCF of 12 and 18 is 6.
Determining the GCF of 10 and 35: Different Methods
Let's tackle the specific question: What is the GCF of 10 and 35? We'll explore several methods to find the answer, each offering a unique approach and understanding of the concept.
Method 1: Listing Factors
This is the most straightforward method, particularly useful for smaller numbers.
- List the factors of 10: 1, 2, 5, 10
- List the factors of 35: 1, 5, 7, 35
- Identify common factors: Both lists share 1 and 5.
- Determine the greatest common factor: The largest common factor is 5.
Therefore, the GCF of 10 and 35 is $\boxed{5}$.
Method 2: Prime Factorization
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 10: 2 x 5
- Prime factorization of 35: 5 x 7
- Identify common prime factors: Both factorizations contain a 5.
- Multiply the common prime factors: The GCF is the product of the common prime factors. In this case, it's just 5.
Again, the GCF of 10 and 35 is $\boxed{5}$. This method is particularly helpful for larger numbers where listing all factors might be tedious.
Method 3: Euclidean Algorithm
This is an efficient algorithm for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
- Start with the two numbers: 10 and 35
- Subtract the smaller from the larger repeatedly:
- 35 - 10 = 25
- 25 - 10 = 15
- 15 - 10 = 5
- 10 - 5 = 5
- The process stops when both numbers are equal: The GCF is 5.
The Euclidean Algorithm provides a systematic and efficient way to find the GCF, especially for larger numbers where listing factors becomes cumbersome.
Significance and Applications of GCF
Understanding and applying GCFs extends far beyond simple arithmetic exercises. GCFs are essential in various mathematical contexts:
-
Simplifying Fractions: The GCF is crucial for reducing fractions to their simplest form. To simplify a fraction, divide both the numerator and the denominator by their GCF. For example, the fraction 10/35 can be simplified to 2/7 by dividing both the numerator and the denominator by their GCF, which is 5.
-
Solving Equations: GCFs play a role in solving algebraic equations, particularly those involving factorization. Finding the GCF of terms in an equation allows for simplification and easier solution.
-
Geometry: GCFs are used in geometric problems involving area and volume calculations. For instance, when finding the dimensions of the largest square tile that can be used to cover a rectangular floor without any gaps or overlaps, you need to determine the GCF of the floor's length and width.
-
Number Theory: GCFs are a fundamental concept in number theory, used in various proofs and theorems related to prime numbers, divisibility, and other number properties.
-
Computer Science: The Euclidean algorithm for finding the GCF is an essential algorithm in computer science used in cryptography, particularly in RSA encryption which relies heavily on prime numbers and their relationships.
Beyond the Basics: Exploring Further Concepts
While finding the GCF of 10 and 35 is a relatively straightforward task, understanding the broader context of GCFs opens up a world of mathematical possibilities. Let's explore some related concepts:
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of two or more given numbers. GCF and LCM are closely related; their product is equal to the product of the original two numbers. This relationship can be used to solve problems involving fractions and ratios.
-
Modular Arithmetic: GCFs play a vital role in modular arithmetic, which involves operations on remainders. Understanding GCFs is important for solving congruences and other problems in this area.
-
Diophantine Equations: These equations involve finding integer solutions. GCFs often play a crucial role in determining whether a Diophantine equation has solutions and in finding those solutions.
-
Abstract Algebra: GCFs extend into abstract algebra, where the concept generalizes to more abstract mathematical structures.
Conclusion: The Power of Understanding GCFs
Determining the greatest common factor, as demonstrated by finding the GCF of 10 and 35, is not just a basic arithmetic operation. It's a fundamental concept with far-reaching implications in various areas of mathematics and beyond. Mastering different methods for finding GCFs, understanding their significance, and exploring related concepts provides a strong foundation for more advanced mathematical studies and problem-solving. The seemingly simple question, "What is the GCF of 10 and 35?" unveils a world of mathematical richness and practicality. By grasping the underlying principles and their diverse applications, we gain a deeper appreciation for the power and elegance of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 10 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.