What Is The Gcf Of 12 18 And 24
News Co
May 08, 2025 · 6 min read
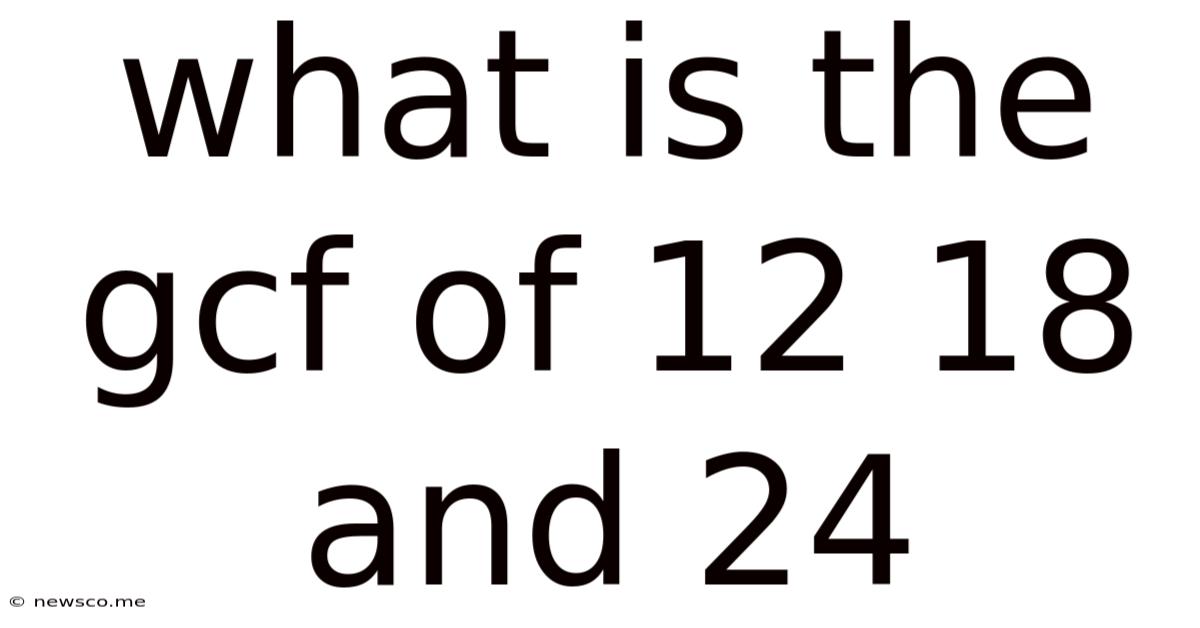
Table of Contents
What is the GCF of 12, 18, and 24? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for various mathematical applications, from simplifying fractions to solving algebraic equations. This comprehensive guide will not only answer the question, "What is the GCF of 12, 18, and 24?" but also equip you with the knowledge and skills to find the GCF of any set of numbers efficiently and accurately.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into all the numbers you're considering without leaving anything leftover.
For example, let's consider the numbers 12, 18, and 24. We want to find the largest number that perfectly divides all three. This number is the GCF.
Methods for Finding the GCF
Several methods can be employed to determine the GCF. We'll explore three common and effective approaches:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to all.
Steps:
-
List the factors of each number:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
-
Identify common factors: Look for the numbers that appear in all three lists. In this case, the common factors are 1, 2, 3, and 6.
-
Determine the greatest common factor: The largest number among the common factors is the GCF. Therefore, the GCF of 12, 18, and 24 is 6.
This method works well for smaller numbers, but it becomes less efficient as the numbers get larger and have more factors.
2. Prime Factorization Method
This method uses the prime factorization of each number to find the GCF. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Steps:
-
Find the prime factorization of each number:
- 12 = 2 x 2 x 3 = 2² x 3
- 18 = 2 x 3 x 3 = 2 x 3²
- 24 = 2 x 2 x 2 x 3 = 2³ x 3
-
Identify common prime factors: Look for the prime factors that appear in all the factorizations. In this case, both 2 and 3 are common.
-
Determine the lowest power of each common prime factor: For each common prime factor, choose the lowest power present in the factorizations. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹.
-
Multiply the lowest powers of the common prime factors: Multiply the lowest powers together to find the GCF. In this case, 2 x 3 = 6. Therefore, the GCF of 12, 18, and 24 is 6.
The prime factorization method is generally more efficient than the listing factors method, especially for larger numbers.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF. For multiple numbers, we apply it iteratively.
Steps:
-
Find the GCF of the first two numbers (12 and 18):
- 18 = 12 x 1 + 6 (18 divided by 12 leaves a remainder of 6)
- 12 = 6 x 2 + 0 (12 divided by 6 leaves a remainder of 0) The GCF of 12 and 18 is 6.
-
Find the GCF of the result (6) and the next number (24):
- 24 = 6 x 4 + 0 (24 divided by 6 leaves a remainder of 0) The GCF of 6 and 24 is 6.
Therefore, the GCF of 12, 18, and 24 is 6.
The Euclidean algorithm is particularly efficient for large numbers because it avoids the need for complete factorization.
Applications of GCF
Understanding and calculating the GCF has numerous applications across various fields:
-
Simplifying fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 12/24 can be simplified to 1/2 by dividing both the numerator and denominator by their GCF, which is 12.
-
Solving algebraic equations: GCF plays a crucial role in factoring algebraic expressions, which simplifies the process of solving equations.
-
Geometry and Measurement: The GCF is used in solving problems related to area, volume, and other geometric calculations. For instance, finding the largest square tile that can perfectly cover a rectangular floor involves determining the GCF of the floor's dimensions.
-
Number Theory: GCF is a fundamental concept in number theory, forming the basis for various theorems and algorithms.
-
Computer Science: The Euclidean algorithm, used to find the GCF, is implemented in computer programs for various cryptographic applications and other computational tasks.
Beyond the Basics: Extending GCF Concepts
While we've focused on finding the GCF of positive integers, the concept extends to other areas:
-
GCF of polynomials: The GCF can also be applied to polynomials (algebraic expressions with variables and coefficients). The process involves finding the greatest common factor among the terms of the polynomial.
-
GCF of fractions: While not directly applicable in the same way as integers, the concept of finding common factors is crucial when working with fractions. The process involves finding the GCF of the numerators and denominators separately, facilitating simplification.
-
Least Common Multiple (LCM): Closely related to the GCF is the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of all the given integers. The GCF and LCM are related by the formula:
LCM(a, b) x GCF(a, b) = a x b.
Conclusion: Mastering GCF
Finding the greatest common factor is a fundamental skill in mathematics with wide-ranging applications. Understanding the different methods—listing factors, prime factorization, and the Euclidean algorithm—allows you to choose the most efficient approach depending on the numbers involved. By mastering these techniques, you build a strong foundation for tackling more advanced mathematical concepts and real-world problems where finding the GCF is crucial. Remember, the key is to choose the method that best suits your needs and the complexity of the numbers you're working with. Practice will make you proficient in identifying and calculating the GCF quickly and accurately. From simplifying fractions to solving complex equations, the GCF proves to be an invaluable tool in the world of mathematics and beyond.
Latest Posts
Latest Posts
-
What Is The Reciprocal Of 5 7
May 08, 2025
-
Does Even Or Odd Numbers Have More Factors
May 08, 2025
-
What Is Diameter Of A Rectangle
May 08, 2025
-
What Is 7 4 7 As An Improper Fraction
May 08, 2025
-
How Is A Parallelogram Different From A Rhombus
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 12 18 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.