What Is The Gcf Of 15 And 21
News Co
Mar 20, 2025 · 5 min read
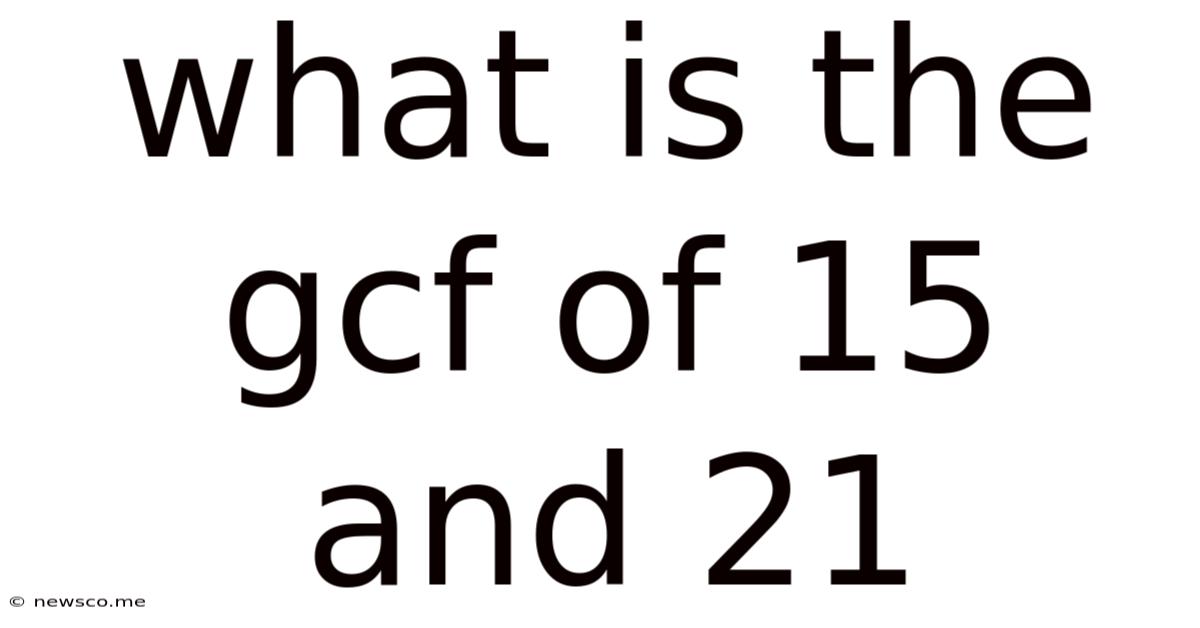
Table of Contents
What is the GCF of 15 and 21? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for solving it opens doors to more advanced mathematical concepts. This comprehensive guide will explore the GCF of 15 and 21, demonstrating multiple approaches and highlighting the broader significance of GCFs in mathematics.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. Understanding GCFs is crucial in various mathematical fields, from simplifying fractions to solving algebraic equations.
Why are GCFs Important?
GCFs are fundamental in simplifying fractions. When you reduce a fraction to its simplest form, you're essentially dividing both the numerator and the denominator by their GCF. For example, simplifying 12/18 involves finding the GCF of 12 and 18 (which is 6) and dividing both by 6, resulting in the simplified fraction 2/3.
GCFs also play a role in solving equations involving variables. Finding the GCF of coefficients in an equation can help simplify and solve it more efficiently.
Furthermore, GCFs are a building block for understanding more complex mathematical concepts like least common multiples (LCMs), which are crucial in various applications, including scheduling and problem-solving.
Methods for Finding the GCF of 15 and 21
Let's now explore several methods to determine the GCF of 15 and 21.
1. Listing Factors Method
This method involves listing all the factors of each number and identifying the largest factor they have in common.
- Factors of 15: 1, 3, 5, 15
- Factors of 21: 1, 3, 7, 21
Comparing the lists, we see that the common factors are 1 and 3. The greatest of these common factors is 3. Therefore, the GCF of 15 and 21 is 3.
This method works well for smaller numbers but can become cumbersome with larger numbers.
2. Prime Factorization Method
This is a more efficient method, particularly for larger numbers. It involves finding the prime factorization of each number and then multiplying the common prime factors raised to the lowest power.
- Prime factorization of 15: 3 x 5
- Prime factorization of 21: 3 x 7
The only common prime factor is 3. Therefore, the GCF of 15 and 21 is 3.
This method is generally more efficient and systematic than listing all factors, especially when dealing with larger numbers that have many factors.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 15 and 21:
- 21 - 15 = 6 (We replace 21 with 6)
- Now we find the GCF of 15 and 6.
- 15 - 6 = 9 (We replace 15 with 9)
- Now we find the GCF of 9 and 6.
- 9 - 6 = 3 (We replace 9 with 3)
- Now we find the GCF of 6 and 3.
- 6 - 3 = 3 (We replace 6 with 3)
- Now we have 3 and 3. Since they are equal, the GCF is 3.
The Euclidean algorithm provides a systematic and efficient approach, especially useful when dealing with larger numbers where listing factors or prime factorization becomes less practical.
Applications of GCFs beyond Basic Arithmetic
The seemingly simple concept of the GCF finds its application in a wide array of mathematical and real-world scenarios. Let's explore some of these:
1. Simplifying Fractions
As previously mentioned, the GCF is essential for simplifying fractions to their lowest terms. This is crucial for easier calculations and understanding the magnitude of the fraction. For example, the fraction 21/15 can be simplified to 7/5 by dividing both the numerator and the denominator by their GCF, which is 3.
2. Solving Algebraic Equations
GCFs can simplify algebraic expressions. Consider an expression like 15x + 21y. The GCF of 15 and 21 is 3. We can factor out the GCF to simplify the expression: 3(5x + 7y). This simplification makes it easier to work with the expression in more complex algebraic manipulations.
3. Geometry and Measurement
GCFs are used in solving geometrical problems involving area and perimeter calculations, particularly when dealing with rectangles or other shapes with dimensions that share common factors.
4. Scheduling and Pattern Recognition
Determining when events will coincide relies on finding the LCM, which is closely related to the GCF. For instance, if one event happens every 15 days and another every 21 days, the LCM of 15 and 21 (which is 105) determines when both events will occur on the same day. The calculation of the LCM utilizes the GCF.
5. Cryptography and Number Theory
More advanced applications of GCFs extend into number theory and cryptography. Algorithms like the RSA encryption algorithm, which is widely used for secure online communications, rely on the properties of GCFs and prime numbers.
Conclusion: The Power of a Simple Concept
The seemingly simple task of finding the greatest common factor of 15 and 21—which we've shown to be 3—illustrates the importance of fundamental mathematical concepts. The various methods discussed—listing factors, prime factorization, and the Euclidean algorithm—highlight the different approaches to solving the same problem, each with its own advantages and disadvantages. The importance of the GCF extends far beyond basic arithmetic, influencing numerous areas of mathematics, particularly number theory and algebra. Understanding GCFs is crucial for developing a strong foundation in mathematics and appreciating the interconnectedness of mathematical concepts. From simplifying fractions to its application in sophisticated encryption techniques, the GCF proves to be a powerful and versatile tool in the world of numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 15 And 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.