What Is The Gcf Of 21 And 18
News Co
Apr 03, 2025 · 6 min read
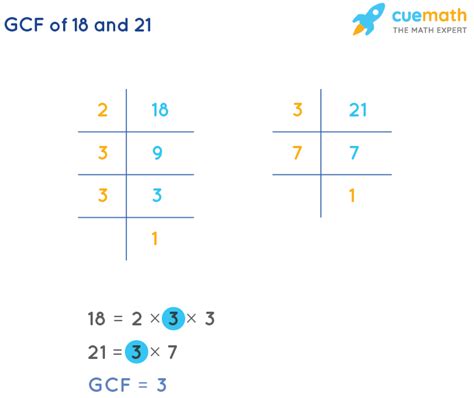
Table of Contents
What is the GCF of 21 and 18? A Deep Dive into Greatest Common Factor
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it is crucial for a strong foundation in mathematics. This article will explore the GCF of 21 and 18 in detail, going beyond just the answer to delve into the "why" and "how" of finding the greatest common factor, and applying this understanding to more complex scenarios.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding this definition is key to grasping the significance of the GCF in various mathematical applications.
Let's consider our example: What is the GCF of 21 and 18? This means we are looking for the largest number that perfectly divides both 21 and 18.
Methods for Finding the GCF
Several methods can be employed to determine the GCF of two or more numbers. Let's explore the most common ones, applying them to find the GCF of 21 and 18:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 21: 1, 3, 7, 21
- Factors of 18: 1, 2, 3, 6, 9, 18
Comparing the two lists, we can see that the common factors are 1 and 3. The largest of these common factors is 3. Therefore, the GCF of 21 and 18 is 3. This method is straightforward for smaller numbers, but it becomes less efficient as the numbers get larger.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then multiplying the common prime factors raised to the lowest power.
- Prime factorization of 21: 3 x 7
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
The common prime factor is 3. The lowest power of 3 in the factorizations is 3¹ (or simply 3). Therefore, the GCF of 21 and 18 is 3. This method is generally more efficient for larger numbers, as it systematically breaks down the numbers into their prime components.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 21 and 18:
- 21 - 18 = 3
- Now we find the GCF of 18 and 3.
- 18 ÷ 3 = 6 with no remainder.
Since 3 divides 18 evenly, the GCF of 21 and 18 is 3. The Euclidean algorithm is significantly more efficient than the previous methods when dealing with larger numbers, as it avoids the need to list all factors or perform extensive prime factorization.
Applications of GCF
The concept of GCF has numerous applications in various fields, including:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 18/21 can be simplified by dividing both the numerator and the denominator by their GCF (3), resulting in the equivalent fraction 6/7.
-
Solving Word Problems: Many word problems involving equal sharing or grouping require finding the GCF to determine the maximum number of equal groups or shares that can be created. For example, if you have 21 apples and 18 oranges, and you want to create identical gift bags with the same number of apples and oranges in each, the GCF (3) will tell you can create 3 gift bags, each with 7 apples and 6 oranges.
-
Geometry: The GCF is useful in geometry problems involving dividing shapes into smaller identical shapes. For instance, finding the dimensions of the largest square that can tile a rectangle with dimensions 21 units by 18 units would involve finding the GCF of 21 and 18.
-
Algebra: GCF is fundamental in factoring algebraic expressions. It's the first step in simplifying complex algebraic equations.
-
Computer Science: The GCF plays a role in various algorithms related to number theory and cryptography.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For instance, to find the GCF of 21, 18, and 15:
-
Prime Factorization Method:
- Prime factorization of 21: 3 x 7
- Prime factorization of 18: 2 x 3²
- Prime factorization of 15: 3 x 5
The only common prime factor is 3, and the lowest power is 3¹. Therefore, the GCF of 21, 18, and 15 is 3.
-
Euclidean Algorithm (Extension): The Euclidean algorithm can be extended by iteratively finding the GCF of pairs of numbers. First find the GCF of two numbers, then find the GCF of that result and the remaining number.
Real-World Examples Illustrating GCF
Let's explore some real-world scenarios that demonstrate the practicality of understanding and applying the GCF:
-
Baking: Imagine you're baking cookies and you have 21 chocolate chips and 18 raisins. You want to distribute these evenly amongst your cookies, such that each cookie has the same number of chocolate chips and raisins. The GCF of 21 and 18 (3) tells you that you can make 3 cookies, each with 7 chocolate chips and 6 raisins.
-
Gardening: You have two rectangular flowerbeds. One measures 21 feet by 18 feet, and you want to divide both flowerbeds into square plots of the same size using the largest possible square. The GCF of 21 and 18 (3) determines the size of the largest possible square plot (3 feet x 3 feet) that can be used for both flowerbeds.
-
Classroom Activity: A teacher has 21 red crayons and 18 blue crayons. She wants to divide the crayons equally among her students, giving each student the same number of red and blue crayons. The GCF (3) shows that she can divide the crayons among 3 students, with each receiving 7 red and 6 blue crayons.
These examples highlight the everyday relevance of understanding the GCF. It's not merely an abstract mathematical concept but a practical tool with wide-ranging applications.
Conclusion: Mastering GCF for Mathematical Proficiency
Understanding the concept of the greatest common factor is foundational to various mathematical applications. Whether you're simplifying fractions, solving word problems, or tackling more advanced algebraic concepts, a firm grasp of the GCF and its various calculation methods is essential. We've explored different methods – listing factors, prime factorization, and the Euclidean algorithm – providing you with versatile tools to find the GCF, regardless of the numbers' size. Remember, the choice of method often depends on the numbers involved, with the Euclidean algorithm proving particularly efficient for larger numbers. By mastering these techniques, you'll enhance your mathematical skills and broaden your ability to tackle a range of problems effectively. The seemingly simple question, "What is the GCF of 21 and 18?" opens up a pathway to a deeper understanding of fundamental mathematical principles and their practical applications in diverse contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 21 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.