What Is The Gcf Of 32 And 45
News Co
Mar 26, 2025 · 5 min read
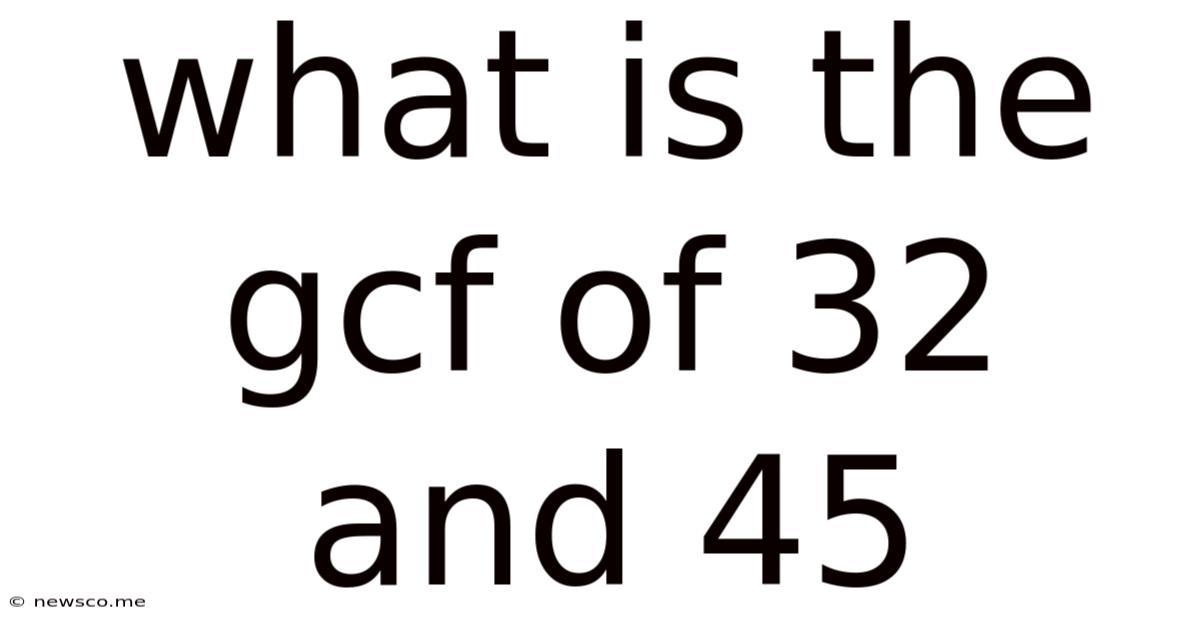
Table of Contents
What is the GCF of 32 and 45? A Deep Dive into Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods opens up a world of mathematical possibilities. This article will explore the GCF of 32 and 45 in detail, providing multiple approaches to solving the problem and highlighting the broader significance of GCF in various mathematical applications.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. This concept is fundamental in number theory and has practical applications in areas like simplifying fractions, solving algebraic equations, and even in computer science algorithms.
Why is finding the GCF important?
Understanding the GCF is crucial for several reasons:
-
Simplifying Fractions: The GCF allows us to reduce fractions to their simplest form. For example, if we have the fraction 16/24, finding the GCF (which is 8) lets us simplify it to 2/3.
-
Solving Equations: In algebra, finding the GCF can be essential for factoring polynomials and solving equations.
-
Understanding Number Relationships: It helps us understand the relationships between numbers, revealing patterns and common divisors.
-
Applications in Computer Science: GCF algorithms are used in various computer science applications, including cryptography and data structure optimization.
Methods for Finding the GCF of 32 and 45
Now, let's delve into finding the GCF of 32 and 45 using several methods.
1. Listing Factors Method
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest factor they share.
Factors of 32: 1, 2, 4, 8, 16, 32 Factors of 45: 1, 3, 5, 9, 15, 45
Comparing the lists, we see that the only common factor is 1.
Therefore, the GCF of 32 and 45 is 1.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors. The GCF is then found by multiplying the common prime factors raised to their lowest powers.
Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup> Prime factorization of 45: 3 x 3 x 5 = 3<sup>2</sup> x 5
There are no common prime factors between 32 and 45. Therefore, their only common factor is 1.
Hence, the GCF of 32 and 45 is 1.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors becomes cumbersome. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 32 and 45:
- 45 = 32 x 1 + 13 (We divide 45 by 32, the remainder is 13)
- 32 = 13 x 2 + 6 (We divide 32 by 13, the remainder is 6)
- 13 = 6 x 2 + 1 (We divide 13 by 6, the remainder is 1)
- 6 = 1 x 6 + 0 (We divide 6 by 1, the remainder is 0)
The last non-zero remainder is 1. Therefore, the GCF of 32 and 45 is 1.
Relatively Prime Numbers
When the GCF of two numbers is 1, as we've found with 32 and 45, the numbers are called relatively prime, coprime, or mutually prime. This means they share no common factors other than 1. This is a significant property in number theory and has various applications in other mathematical fields.
Expanding on the Concept: GCF in Different Contexts
The concept of the GCF extends beyond just finding the greatest common factor of two integers. Let's explore some broader applications:
GCF of Polynomials
The concept of GCF also applies to polynomials. We can find the greatest common factor of two or more polynomials by identifying the greatest common factor of their coefficients and variables. This is crucial in simplifying polynomial expressions and solving algebraic equations.
GCF in Real-World Applications
While finding the GCF of 32 and 45 might seem abstract, the concept underlies many practical applications:
-
Dividing Resources: Imagine dividing 32 apples and 45 oranges equally among several people. The GCF (which is 1 in this case) implies that we can only distribute the fruits in groups of one.
-
Scheduling: The GCF is used in scheduling problems to find the least common multiple (LCM) – the smallest number divisible by both numbers. The LCM is relevant to finding the time interval when two repeating events will coincide.
-
Construction: In construction, the GCF can be used in calculating dimensions and proportions to optimize the use of materials.
-
Data Compression: In computer science, GCF is utilized in algorithms for data compression and encoding to achieve higher efficiency.
Conclusion: Beyond the Calculation
Finding the GCF of 32 and 45, although resulting in a simple answer (1), provides a stepping stone to understanding fundamental concepts in number theory. Mastering these techniques opens doors to more complex mathematical problems and real-world applications. The methods discussed – listing factors, prime factorization, and the Euclidean algorithm – demonstrate that even a seemingly basic arithmetic problem can have numerous approaches and underlying significance. Understanding the GCF isn't merely about solving for a number; it’s about grasping the underlying principles that govern numerical relationships and their broader implications across various fields. This understanding provides a solid foundation for tackling more complex mathematical challenges and appreciating the beauty and utility of mathematical concepts in our daily lives.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 32 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.