What Is The Gcf Of 48 And 80
News Co
Mar 17, 2025 · 6 min read
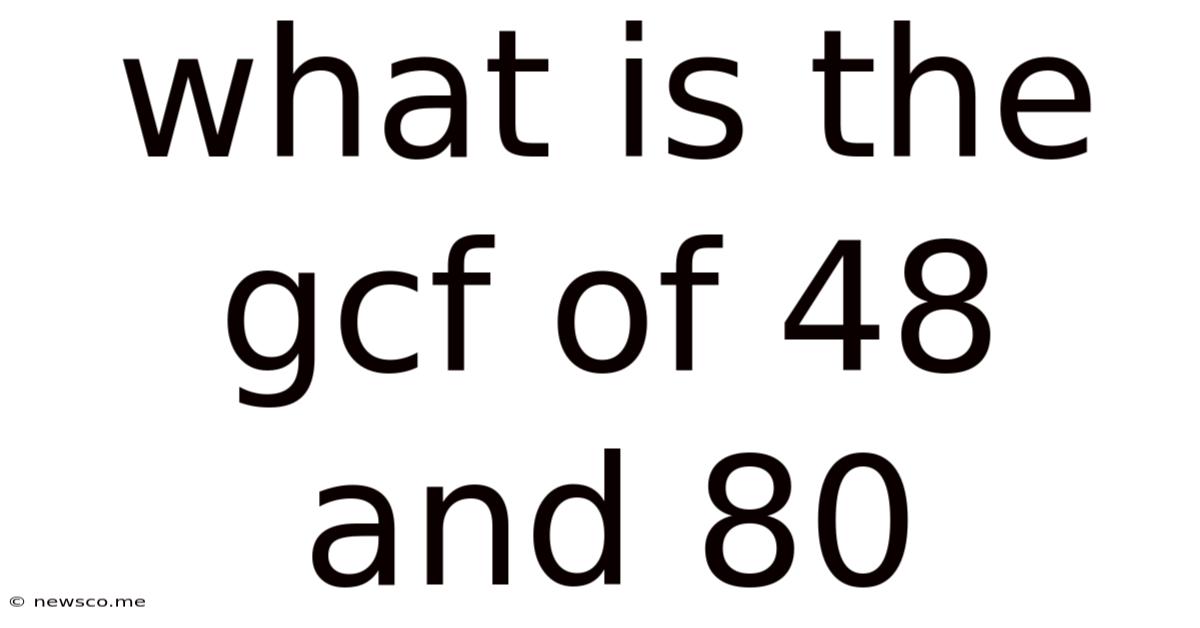
Table of Contents
What is the GCF of 48 and 80? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it opens up a world of mathematical possibilities. This comprehensive guide will explore the GCF of 48 and 80, detailing various approaches and highlighting their practical applications. We'll go beyond a simple answer and delve into the "why" behind the calculations, making this a valuable resource for students and anyone interested in strengthening their number theory skills.
Understanding Greatest Common Factors (GCF)
Before jumping into the specifics of 48 and 80, let's solidify our understanding of GCFs. The greatest common factor (also known as the greatest common divisor or GCD) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers.
Example: The GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Understanding GCFs is crucial in various mathematical contexts, including:
- Simplifying fractions: Finding the GCF of the numerator and denominator allows you to reduce a fraction to its simplest form.
- Solving algebraic equations: GCFs play a role in factoring polynomials and simplifying algebraic expressions.
- Geometry and measurement: GCFs are used in problems involving dividing shapes into equal parts or finding the dimensions of objects with specific constraints.
Methods for Finding the GCF of 48 and 80
Several methods can be used to determine the GCF of 48 and 80. Let's explore the most common ones:
1. Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 Factors of 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Comparing the two lists, we can see that the common factors are 1, 2, 4, 8, and 16. The largest of these common factors is 16. Therefore, the GCF of 48 and 80 is 16.
This method is straightforward for smaller numbers but can become cumbersome with larger numbers.
2. Prime Factorization
This method uses the prime factorization of each number to find the GCF. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Prime factorization of 48: 2 x 2 x 2 x 2 x 3 = 2⁴ x 3 Prime factorization of 80: 2 x 2 x 2 x 2 x 5 = 2⁴ x 5
To find the GCF, identify the common prime factors and their lowest powers. Both 48 and 80 share four factors of 2 (2⁴). There are no other common prime factors. Therefore, the GCF is 2⁴ = 16.
This method is generally more efficient than listing factors, especially for larger numbers.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to 48 and 80:
- 80 - 48 = 32 (Now we find the GCF of 48 and 32)
- 48 - 32 = 16 (Now we find the GCF of 32 and 16)
- 32 - 16 = 16 (Now we find the GCF of 16 and 16)
Since both numbers are now 16, the GCF of 48 and 80 is 16.
The Euclidean algorithm is particularly useful for large numbers because it avoids the need to find all factors.
Applications of GCFs: Real-World Examples
The concept of GCFs extends beyond theoretical mathematics; it finds practical application in various real-world scenarios. Here are a few examples:
-
Dividing Objects Equally: Imagine you have 48 apples and 80 oranges, and you want to divide them into identical bags such that each bag contains the same number of apples and oranges. The GCF (16) tells you that you can make 16 identical bags, each containing 3 apples (48/16) and 5 oranges (80/16).
-
Simplifying Fractions: If you have a fraction like 48/80, finding the GCF allows you to simplify it. Dividing both the numerator and denominator by the GCF (16), you get the equivalent fraction 3/5.
-
Tiling and Pattern Design: GCFs can be used to determine the size of the largest square tile that can perfectly cover a rectangular area without any gaps or overlaps. If you have a rectangular area of 48 units by 80 units, the largest square tile you can use is 16 units by 16 units.
-
Music and Rhythm: GCFs are used in music theory to determine the greatest common divisor of note durations, which helps in understanding rhythmic relationships and simplifying musical notation.
Beyond the Basics: Extending the Concept of GCF
The concept of GCFs can be extended to more than two numbers. To find the GCF of multiple numbers, you can use any of the methods described above, applying them iteratively. For instance, to find the GCF of 48, 80, and 120, you would first find the GCF of 48 and 80 (which is 16), and then find the GCF of 16 and 120.
Furthermore, the concept of GCFs forms the foundation for understanding other important mathematical concepts like the least common multiple (LCM). The LCM is the smallest number that is a multiple of two or more integers. There is a relationship between the GCF and LCM: For any two integers 'a' and 'b', the product of their GCF and LCM is equal to the product of the two numbers (GCF(a,b) * LCM(a,b) = a * b). This relationship is frequently used in solving problems involving fractions and ratios.
Conclusion: Mastering GCFs for Mathematical Proficiency
Mastering the calculation of greatest common factors is a cornerstone of mathematical proficiency. The ability to efficiently determine GCFs, using methods like prime factorization or the Euclidean algorithm, opens doors to solving more complex problems in various fields. This guide has explored multiple approaches to finding the GCF of 48 and 80, demonstrating the versatility and practical applications of this fundamental concept. By understanding the underlying principles and practicing these methods, you'll build a stronger foundation in number theory and enhance your problem-solving skills. Remember, the journey of mathematical understanding is a continuous process of exploration and application, and the GCF is just one exciting step along the way.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 48 And 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.