What Is The Gcf Of 64 And 72
News Co
Mar 28, 2025 · 5 min read
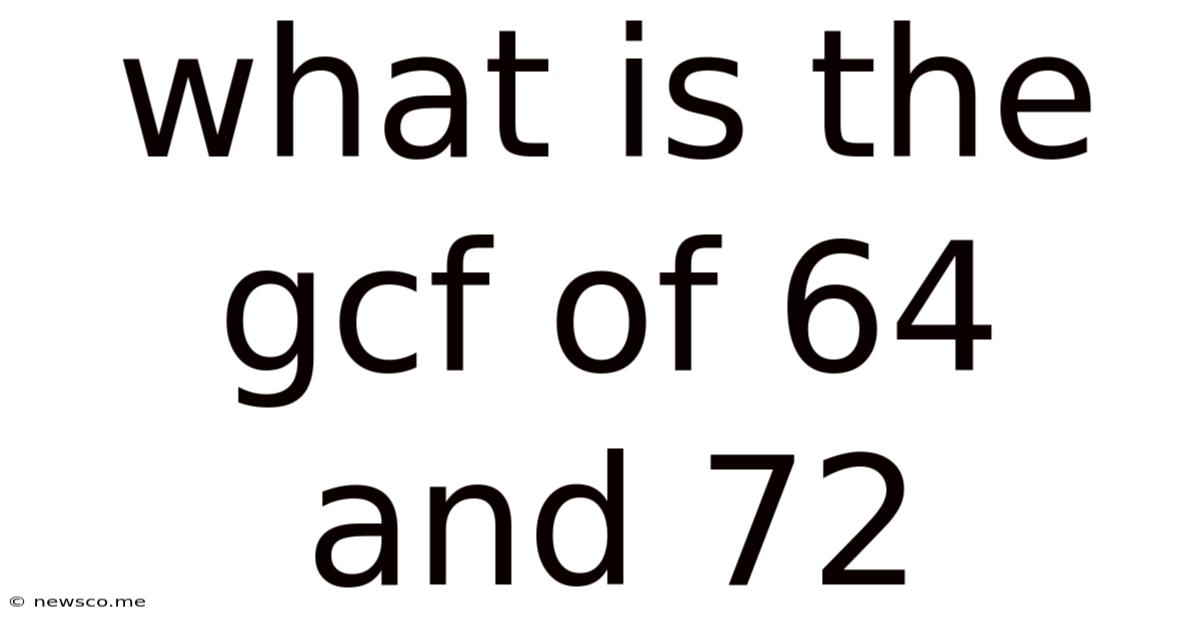
Table of Contents
What is the GCF of 64 and 72? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and various methods can be incredibly valuable, especially when tackling more complex problems in algebra and beyond. This article delves deep into determining the GCF of 64 and 72, exploring multiple approaches and highlighting the significance of GCF in various mathematical contexts.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers perfectly. Understanding the GCF is fundamental in simplifying fractions, solving equations, and tackling more advanced mathematical concepts.
Let's consider our target numbers: 64 and 72. Before jumping into methods, let's list the factors of each number:
Factors of 64: 1, 2, 4, 8, 16, 32, 64 Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
By inspecting these lists, we can visually identify the common factors: 1, 2, 4, and 8. The largest of these is 8. Therefore, the GCF of 64 and 72 is 8. However, this method becomes increasingly cumbersome with larger numbers. Let's explore more efficient techniques.
Method 1: Prime Factorization
Prime factorization is a powerful method for finding the GCF, particularly effective for larger numbers. It involves expressing each number as a product of its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 64:
64 = 2 x 32 = 2 x 2 x 16 = 2 x 2 x 2 x 8 = 2 x 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 x 2 = 2<sup>6</sup>
Prime Factorization of 72:
72 = 2 x 36 = 2 x 2 x 18 = 2 x 2 x 2 x 9 = 2 x 2 x 2 x 3 x 3 = 2<sup>3</sup> x 3<sup>2</sup>
Once we have the prime factorizations, we identify the common prime factors and their lowest powers. Both 64 and 72 share the prime factor 2. The lowest power of 2 present in both factorizations is 2<sup>3</sup> (or 8). Therefore, the GCF is 2<sup>3</sup> = 8.
Method 2: Euclidean Algorithm
The Euclidean algorithm is an elegant and efficient method for finding the GCF, especially when dealing with larger numbers. This method relies on repeated division until the remainder is zero. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to 64 and 72:
-
Divide the larger number (72) by the smaller number (64): 72 ÷ 64 = 1 with a remainder of 8
-
Replace the larger number with the smaller number (64) and the smaller number with the remainder (8): 64 ÷ 8 = 8 with a remainder of 0
Since the remainder is 0, the GCF is the last non-zero remainder, which is 8.
Method 3: Listing Factors (Suitable for Smaller Numbers)
While less efficient for larger numbers, listing factors can be a straightforward approach for smaller numbers like 64 and 72. We already performed this method earlier. We listed all the factors of 64 and 72 and identified the common factors. The greatest of these common factors is the GCF. This method is easily understood but becomes impractical for large numbers.
The Significance of GCF
The GCF isn't merely an abstract mathematical concept; it has practical applications in various fields:
-
Simplifying Fractions: Finding the GCF allows us to reduce fractions to their simplest form. For instance, if we have the fraction 72/64, finding the GCF (8) enables us to simplify the fraction to 9/8.
-
Solving Equations: GCF plays a role in solving certain types of equations, particularly those involving factoring.
-
Geometry: GCF can be utilized in geometric problems involving the dimensions of shapes. For example, finding the largest square tile that can perfectly cover a rectangular floor requires calculating the GCF of the floor's dimensions.
-
Number Theory: GCF is a fundamental concept in number theory, underpinning various theorems and proofs.
Extending the Concept: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of each of the integers. Finding both the GCF and LCM is frequently necessary in solving mathematical problems.
For 64 and 72:
- GCF (64, 72) = 8
- LCM (64, 72) = 576
There's a useful relationship between the GCF and LCM of two numbers (a and b):
GCF(a, b) * LCM(a, b) = a * b
In our case: 8 * 576 = 4608 = 64 * 72. This relationship provides a quick way to find the LCM if you already know the GCF, or vice versa.
Conclusion: Mastering GCF for Mathematical Proficiency
Finding the greatest common factor of 64 and 72, as demonstrated through prime factorization, the Euclidean algorithm, and listing factors, is a fundamental skill in mathematics. Understanding different methods allows you to choose the most efficient approach depending on the complexity of the numbers. The GCF's applications extend far beyond simple arithmetic, proving essential in various mathematical disciplines and practical problem-solving scenarios. By mastering the concept of GCF, you'll build a solid foundation for tackling more complex mathematical challenges. Remember to practice regularly to solidify your understanding and increase your proficiency. The more you work with GCF problems, the more intuitive the process will become. And don't hesitate to explore further mathematical concepts – the world of numbers is vast and full of fascinating discoveries!
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 64 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.