What Is The Gcf Of 7 And 28
News Co
Mar 27, 2025 · 5 min read
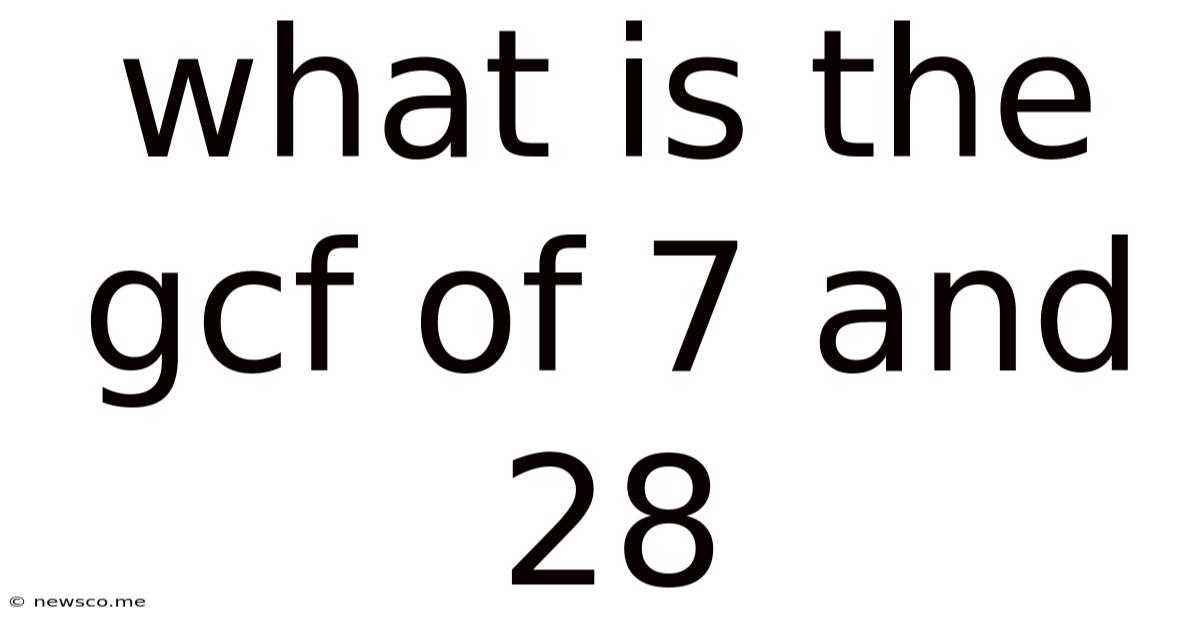
Table of Contents
What is the GCF of 7 and 28? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for solving it opens doors to more complex mathematical ideas. This article will explore the GCF of 7 and 28 in detail, explaining not just the answer but the 'why' behind the process. We'll delve into different methods, highlighting their strengths and weaknesses, and ultimately demonstrate how finding the GCF extends to more advanced mathematical concepts.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific problem of finding the GCF of 7 and 28, let's establish a solid foundation. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
Consider two numbers, 'a' and 'b'. Their GCF is the largest number 'x' such that 'a' is divisible by 'x' and 'b' is divisible by 'x'. This concept is crucial in various mathematical areas, including simplifying fractions, solving algebraic equations, and understanding number theory.
Method 1: Listing Factors
The most straightforward method for finding the GCF is by listing all the factors of each number and then identifying the largest common factor.
Factors of 7: 1, 7
Factors of 28: 1, 2, 4, 7, 14, 28
Comparing the lists, we see that the common factors of 7 and 28 are 1 and 7. The greatest of these common factors is 7. Therefore, the GCF of 7 and 28 is 7.
This method is effective for smaller numbers, but it becomes cumbersome and time-consuming as the numbers increase in size. Imagine trying this method with much larger numbers; the list of factors could be incredibly lengthy.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, is prime factorization. This involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime factorization of 7: 7 (7 is a prime number itself)
Prime factorization of 28: 2 x 2 x 7 (or 2² x 7)
Once we have the prime factorizations, we identify the common prime factors and multiply them together. In this case, the only common prime factor is 7. Therefore, the GCF of 7 and 28 is 7.
This method is superior to listing factors because it's systematic and efficient, even with larger numbers. The prime factorization provides a clear and concise representation of the number's structure, making it easier to identify common factors.
Method 3: Euclidean Algorithm
For larger numbers, the Euclidean Algorithm provides a highly efficient method for finding the GCF. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean Algorithm to 7 and 28:
- Subtract the smaller number (7) from the larger number (28): 28 - 7 = 21
- Now we find the GCF of 7 and 21:
- Subtract 7 from 21: 21 - 7 = 14
- Subtract 7 from 14: 14 - 7 = 7
- Now we have 7 and 7. They are equal.
Therefore, the GCF of 7 and 28 is 7.
The Euclidean Algorithm is particularly useful for larger numbers because it avoids the need to generate extensive lists of factors or perform complex prime factorizations. Its iterative nature makes it computationally efficient.
Why is Understanding GCF Important?
The concept of the greatest common factor extends far beyond basic arithmetic. Here are some key applications:
-
Simplifying Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For example, the fraction 28/7 can be simplified by dividing both the numerator and denominator by their GCF (7), resulting in the simplified fraction 4/1 or simply 4.
-
Solving Algebraic Equations: GCF plays a critical role in factoring algebraic expressions. Factoring allows us to simplify complex equations and solve them more easily.
-
Number Theory: GCF is a fundamental concept in number theory, a branch of mathematics that deals with the properties of integers. It's used in various theorems and proofs, including the Euclidean algorithm itself, which has profound implications in cryptography and computer science.
-
Geometry and Measurement: GCF is used in geometric problems related to finding the largest possible square or cube that can be used to perfectly tile or fill a given area or volume.
-
Real-World Applications: GCF finds practical applications in various fields, such as dividing items into equal groups (e.g., distributing 28 cookies among 7 friends), or determining the dimensions of objects with maximum common factors (e.g., designing tiles for a floor).
Beyond the Basics: Exploring Related Concepts
Understanding GCF naturally leads to exploring related mathematical concepts:
-
Least Common Multiple (LCM): While GCF finds the largest common factor, the LCM finds the smallest common multiple of two or more numbers. GCF and LCM are related through a useful formula: LCM(a, b) x GCF(a, b) = a x b.
-
Modular Arithmetic: GCF is essential in modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value, called the modulus. The GCF is used in operations like finding modular inverses.
-
Diophantine Equations: GCF plays a vital role in solving Diophantine equations, which are algebraic equations where only integer solutions are sought.
-
Cryptography: The Euclidean Algorithm, used for finding GCF, is a cornerstone of many cryptographic algorithms. Its efficiency and mathematical properties make it crucial for secure communication.
Conclusion: The Power of Understanding GCF
Finding the GCF of 7 and 28, while seemingly a simple task, serves as a gateway to understanding fundamental mathematical principles. Mastering different methods for finding the GCF – listing factors, prime factorization, and the Euclidean Algorithm – equips us with tools applicable across various mathematical disciplines and real-world scenarios. The seemingly basic concept of GCF reveals its significant contribution to more advanced topics in number theory, algebra, and even computer science. Therefore, a thorough understanding of GCF isn't merely about finding the answer; it's about grasping a fundamental concept that underpins much of higher mathematics and its applications. The ability to efficiently and accurately determine the GCF empowers you with a powerful tool for tackling more complex mathematical challenges.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 7 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.