What Is The Gcf Of 72 And 120
News Co
Apr 23, 2025 · 5 min read
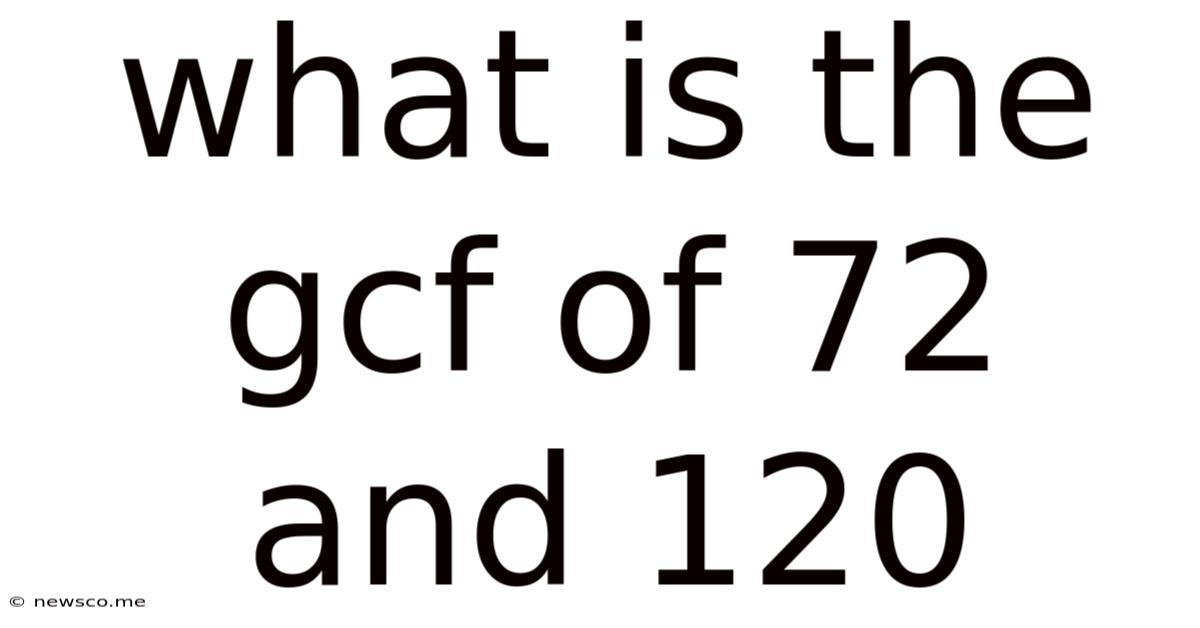
Table of Contents
What is the GCF of 72 and 120? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods involved opens doors to more advanced mathematical concepts. This comprehensive guide will not only answer the question, "What is the GCF of 72 and 120?" but also equip you with the knowledge and skills to tackle similar problems efficiently and effectively. We'll explore multiple approaches, discuss their applications, and highlight the importance of GCF in various mathematical fields.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding the GCF is fundamental in simplifying fractions, solving algebraic equations, and various other mathematical applications.
Methods for Finding the GCF
Several methods exist for determining the GCF of two or more numbers. Let's explore the most common ones:
1. Listing Factors Method
This method is best suited for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 Factors of 120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Comparing the lists, we can see that the common factors are 1, 2, 3, 4, 6, 8, 12, and 24. The greatest of these common factors is 24. Therefore, the GCF of 72 and 120 is 24.
This method becomes cumbersome with larger numbers, making it less efficient for more complex calculations.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors. The GCF is then found by multiplying the common prime factors raised to their lowest powers.
Prime factorization of 72: 2³ x 3² (2 x 2 x 2 x 3 x 3) Prime factorization of 120: 2³ x 3 x 5 (2 x 2 x 2 x 3 x 5)
The common prime factors are 2³ and 3¹. Multiplying these together: 2³ x 3¹ = 8 x 3 = 24.
Therefore, the GCF of 72 and 120 is 24. This method is generally more efficient than listing factors, especially when dealing with larger numbers.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which is the GCF.
Let's apply the Euclidean algorithm to 72 and 120:
- 120 - 72 = 48 (Now we find the GCF of 72 and 48)
- 72 - 48 = 24 (Now we find the GCF of 48 and 24)
- 48 - 24 = 24 (The numbers are now equal)
Therefore, the GCF of 72 and 120 is 24. The Euclidean algorithm is significantly faster than the previous methods for large numbers, as it avoids the need for extensive factorization or listing.
Applications of the GCF
The GCF has wide-ranging applications across various mathematical fields and real-world scenarios:
-
Simplifying Fractions: The GCF is crucial in simplifying fractions to their lowest terms. For example, the fraction 72/120 can be simplified by dividing both the numerator and denominator by their GCF (24), resulting in the simplified fraction 3/5.
-
Solving Algebraic Equations: The GCF plays a vital role in factoring algebraic expressions. Finding the GCF of the terms allows for simplification and easier solution of equations.
-
Geometry: The GCF is used in determining the dimensions of the largest square tile that can be used to cover a rectangular area without any gaps or overlaps.
-
Real-world Applications: GCF concepts find applications in everyday life, such as dividing objects or resources evenly amongst groups, arranging objects in arrays, or planning projects involving repetitive patterns.
Beyond the Basics: GCF of More Than Two Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. For instance, to find the GCF of 72, 120, and 144, we could use the prime factorization method:
- 72: 2³ x 3²
- 120: 2³ x 3 x 5
- 144: 2⁴ x 3²
The common prime factors are 2³ and 3¹. Therefore, the GCF of 72, 120, and 144 is 2³ x 3¹ = 24.
Similarly, the Euclidean algorithm can be adapted to find the GCF of multiple numbers by repeatedly applying the algorithm to pairs of numbers.
Conclusion: Mastering GCF Calculations
Finding the greatest common factor is a fundamental skill in mathematics with far-reaching applications. While simple methods like listing factors suffice for smaller numbers, the prime factorization and Euclidean algorithms provide more efficient approaches for larger numbers. Understanding these different methods allows for flexibility and efficiency in problem-solving. Mastering GCF calculations strengthens your mathematical foundation and empowers you to tackle more complex mathematical challenges with confidence. The GCF of 72 and 120, as demonstrated through various methods, is definitively 24. Remember to choose the method best suited to the numbers involved and the context of the problem. This understanding of GCF is not merely about solving a single problem, but about building a solid mathematical framework for future learning and applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 72 And 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.