What Is The Gcf Of 72 And 84
News Co
Apr 03, 2025 · 5 min read
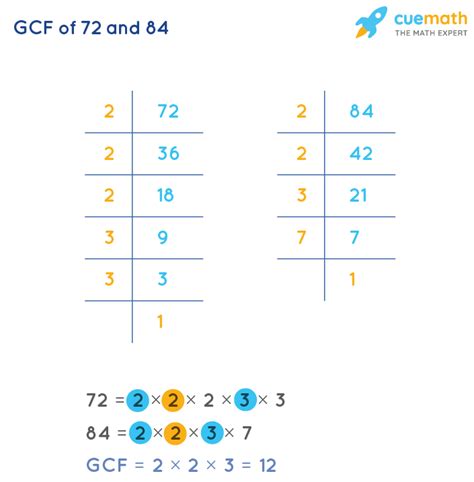
Table of Contents
What is the GCF of 72 and 84? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and various methods can be incredibly valuable, particularly in algebra, number theory, and even everyday problem-solving. This article will explore several ways to determine the GCF of 72 and 84, delving into the methods themselves and highlighting their applications beyond simple calculations.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding the GCF is crucial for simplifying fractions, solving equations, and performing various mathematical operations efficiently.
Method 1: Listing Factors
The most straightforward method to find the GCF is by listing all the factors of each number and then identifying the largest common factor.
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Comparing the two lists, we can see the common factors are: 1, 2, 3, 4, 6, and 12. The greatest of these common factors is 12. Therefore, the GCF of 72 and 84 is 12.
This method works well for smaller numbers, but it becomes increasingly cumbersome as the numbers grow larger. Let's explore more efficient techniques.
Method 2: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This method is more efficient for larger numbers.
Prime factorization of 72:
72 = 2 x 36 = 2 x 2 x 18 = 2 x 2 x 2 x 9 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
Prime factorization of 84:
84 = 2 x 42 = 2 x 2 x 21 = 2 x 2 x 3 x 7 = 2² x 3 x 7
Now, we identify the common prime factors and their lowest powers:
- Both numbers have 2 as a factor. The lowest power of 2 present in both is 2².
- Both numbers have 3 as a factor. The lowest power of 3 present in both is 3¹.
To find the GCF, we multiply these common prime factors raised to their lowest powers:
GCF(72, 84) = 2² x 3¹ = 4 x 3 = 12
This method provides a systematic and efficient approach, even with larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for very large numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 72 and 84:
- Start with the larger number (84) and the smaller number (72).
- Subtract the smaller number from the larger number: 84 - 72 = 12
- Replace the larger number with the result (12) and keep the smaller number (72).
- Repeat the process: 72 - 12 = 60
- Repeat: 60 - 12 = 48
- Repeat: 48 - 12 = 36
- Repeat: 36 - 12 = 24
- Repeat: 24 - 12 = 12
- Now we have 12 and 12. Since they are equal, the GCF is 12.
While this iterative process seems longer than prime factorization for these smaller numbers, its efficiency becomes dramatically apparent when dealing with significantly larger numbers where prime factorization becomes considerably more complex.
Applications of Finding the GCF
The ability to find the GCF extends beyond simple arithmetic exercises. It has practical applications in various fields:
1. Simplifying Fractions:
The GCF is fundamental to simplifying fractions to their lowest terms. To simplify a fraction, divide both the numerator and the denominator by their GCF. For example, if you have the fraction 72/84, dividing both by their GCF (12) simplifies the fraction to 6/7.
2. Solving Equations:
The GCF plays a crucial role in solving certain types of algebraic equations, particularly those involving factoring. Finding the GCF of the terms in an equation allows for simplification and efficient solution-finding.
3. Geometry and Measurement:
The GCF is used in geometry problems involving dividing shapes into equal parts or finding the dimensions of objects with specific constraints. For example, determining the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the floor's length and width.
4. Number Theory:
GCF is a cornerstone concept in number theory, a branch of mathematics that studies the properties of integers. It forms the basis for many theorems and algorithms within the field.
5. Cryptography:
The concept of GCF, specifically the Euclidean algorithm for finding it, underpins certain aspects of cryptography, the practice and study of techniques for secure communication in the presence of adversarial behavior.
Conclusion: Mastering GCF Calculations
Finding the greatest common factor of 72 and 84, as demonstrated, is achievable through several methods. The choice of method depends on the size of the numbers involved and the context of the problem. While listing factors is suitable for small numbers, prime factorization offers a more systematic approach for larger numbers. The Euclidean algorithm emerges as the most efficient method for extremely large numbers, making it a vital tool in advanced mathematical applications. Understanding these methods not only improves arithmetic skills but also provides a strong foundation for tackling more complex mathematical problems across various disciplines. The ability to efficiently determine the GCF is a skill with wide-ranging applications beyond the classroom, highlighting its practical importance in various fields.
Latest Posts
Latest Posts
-
What Is 10 To The 7th Power
Apr 04, 2025
-
How To Make An Improper Fraction Into A Proper Fraction
Apr 04, 2025
-
What Is 5 To The 4th Power
Apr 04, 2025
-
What Is The Square Root Of 71
Apr 04, 2025
-
Inverse Matrix Calculator Step By Step
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 72 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
