What Is The Greatest Common Factor Of 2 And 6
News Co
Mar 24, 2025 · 5 min read
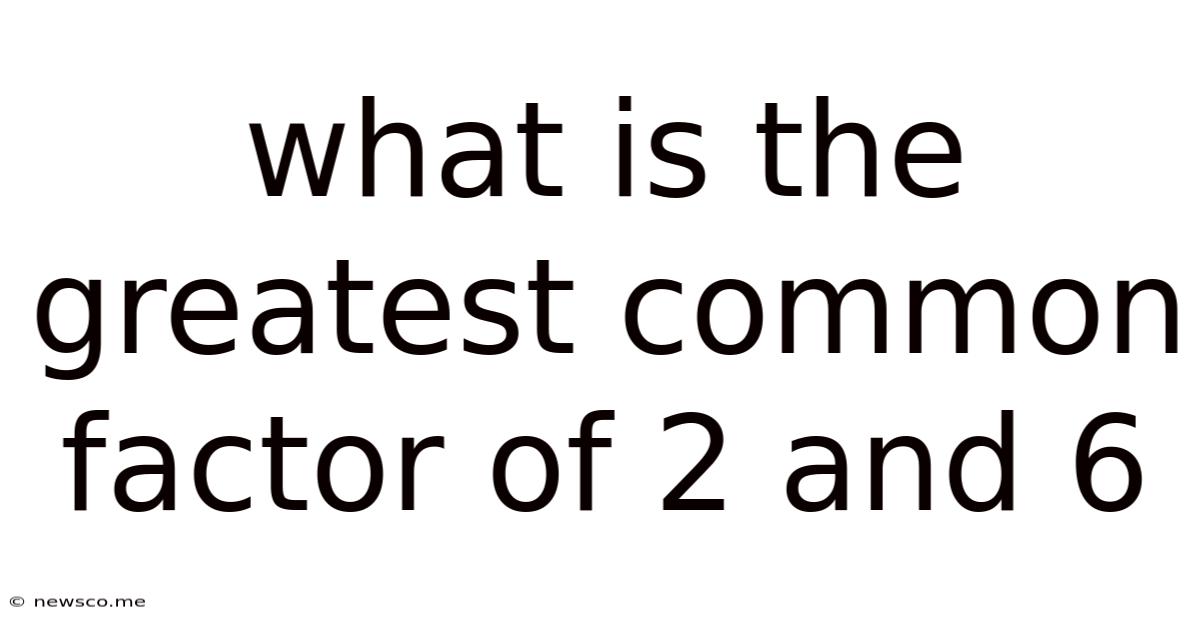
Table of Contents
What is the Greatest Common Factor of 2 and 6? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple task, especially when dealing with small numbers like 2 and 6. However, understanding the underlying principles behind GCF calculations opens the door to a deeper appreciation of number theory and its applications in various fields, from cryptography to computer science. This article will not only answer the question of what the GCF of 2 and 6 is but will also explore various methods for finding the GCF, delve into the significance of GCF in mathematics, and discuss its practical applications.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Identifying Factors
Before we can find the GCF, we need to understand what factors are. Factors are numbers that divide a given number without leaving a remainder. For example, the factors of 6 are 1, 2, 3, and 6. The factors of 12 are 1, 2, 3, 4, 6, and 12.
Finding the GCF of 2 and 6: Methods and Solutions
Now, let's tackle the question at hand: What is the greatest common factor of 2 and 6?
Method 1: Listing Factors
The simplest method to find the GCF is by listing all the factors of each number and then identifying the largest common factor.
- Factors of 2: 1, 2
- Factors of 6: 1, 2, 3, 6
Comparing the two lists, we see that the common factors are 1 and 2. The largest of these common factors is 2. Therefore, the GCF of 2 and 6 is 2.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the GCF of larger numbers. It involves expressing each number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 2: 2 (2 is a prime number)
- Prime factorization of 6: 2 x 3
The common prime factor is 2. Therefore, the GCF is 2.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors becomes cumbersome. The algorithm involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 2 and 6:
- Divide the larger number (6) by the smaller number (2): 6 ÷ 2 = 3 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is the smaller number, 2.
The Significance of GCF in Mathematics
The GCF is a fundamental concept in number theory with far-reaching implications. Its applications extend beyond simple arithmetic problems and play a crucial role in:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 6/12 can be simplified to 1/2 by dividing both the numerator and the denominator by their GCF, which is 6.
-
Solving Diophantine Equations: Diophantine equations are equations where the solutions are restricted to integers. The GCF is often used in finding solutions to these types of equations.
-
Modular Arithmetic: Modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value, called the modulus. The GCF plays a vital role in understanding properties of modular arithmetic, such as finding inverses.
-
Cryptography: Concepts related to GCF, such as the Euclidean algorithm, are used in cryptographic algorithms like RSA, which is widely used for secure communication over the internet. The security of these algorithms relies heavily on the difficulty of factoring large numbers into their prime factors.
Practical Applications of GCF
Beyond its theoretical significance, the GCF has practical applications in various areas:
-
Measurement and Geometry: The GCF is used to find the largest possible square tiles that can be used to cover a rectangular area without any cuts or gaps. For example, if you have a rectangle with dimensions 12 cm and 18 cm, the largest square tile you can use is 6 cm x 6 cm (because the GCF of 12 and 18 is 6).
-
Resource Allocation: The GCF can be used to efficiently divide resources amongst groups. For example, if you have 12 apples and 18 oranges and you want to divide them equally among groups, the largest number of groups you can form is 6 (the GCF of 12 and 18).
Beyond the Basics: Exploring More Complex Scenarios
While finding the GCF of 2 and 6 is straightforward, the concept extends to larger numbers and multiple numbers. The methods we've discussed – listing factors, prime factorization, and the Euclidean algorithm – can all be applied to more complex scenarios.
For example, finding the GCF of three numbers such as 12, 18, and 24 involves finding the GCF of two numbers at a time and iterating:
- Find the GCF of 12 and 18 (which is 6).
- Find the GCF of 6 and 24 (which is 6). Therefore, the GCF of 12, 18, and 24 is 6.
The Euclidean algorithm can also be extended for multiple numbers efficiently.
Conclusion: The Enduring Importance of the Greatest Common Factor
The GCF, seemingly a simple concept at first glance, reveals a rich tapestry of mathematical principles and applications. From simplifying fractions to securing online communications, the GCF demonstrates the power of fundamental mathematical concepts to influence diverse fields. While the GCF of 2 and 6 is simply 2, understanding the methods for calculating it and its broader significance provides a valuable foundation for further exploration in number theory and its practical applications in the real world. The seemingly simple question of finding the GCF of 2 and 6 underscores the beauty and utility of mathematics, revealing how basic concepts can form the bedrock of more complex and impactful ideas.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 2 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.