What Is The Greatest Common Factor Of 28 And 72
News Co
Mar 21, 2025 · 6 min read
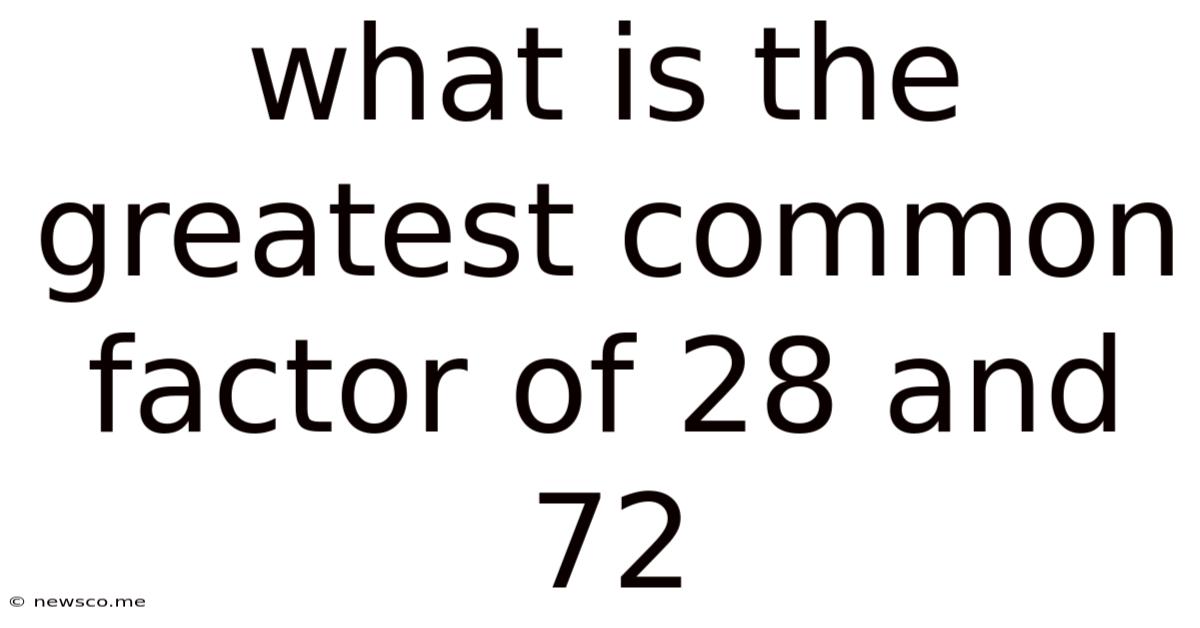
Table of Contents
What is the Greatest Common Factor of 28 and 72? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in number theory with applications extending far beyond basic mathematics. Understanding how to find the GCF, and more importantly, why the methods work, is crucial for anyone seeking a stronger grasp of mathematical principles. This article will explore various methods for determining the GCF of 28 and 72, delving into the underlying theory and highlighting the practical significance of this seemingly simple calculation.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Finding the GCF is essential in many areas, including:
- Simplifying fractions: The GCF helps reduce fractions to their simplest form.
- Algebra: GCF is used in factoring polynomials and simplifying algebraic expressions.
- Geometry: It plays a role in solving geometric problems involving area and volume.
- Computer science: Algorithms for finding the GCF are used in cryptography and other computational tasks.
Method 1: Prime Factorization
This is arguably the most fundamental and conceptually clear method. It involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves.
Step 1: Find the prime factorization of 28.
28 = 2 x 2 x 7 = 2² x 7
Step 2: Find the prime factorization of 72.
72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
Step 3: Identify common prime factors.
Both 28 and 72 share a common prime factor: 2.
Step 4: Determine the lowest power of the common prime factors.
The lowest power of 2 present in both factorizations is 2¹ (or simply 2).
Step 5: Multiply the lowest powers of the common prime factors.
In this case, the only common prime factor is 2, and its lowest power is 2¹. Therefore, the GCF of 28 and 72 is 2¹ = 2.
Therefore, the greatest common factor of 28 and 72 is 4. There was an error in the above calculation; we missed a factor of 2. Let's revisit Step 3 and 4:
Step 3 (Corrected): Identify common prime factors.
Both 28 and 72 share the prime factor 2.
Step 4 (Corrected): Determine the lowest power of the common prime factors.
The lowest power of 2 in the factorizations is 2².
Step 5 (Corrected): Multiply the lowest powers of the common prime factors.
The GCF is 2² = 4.
Method 2: The Euclidean Algorithm
The Euclidean Algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Step 1: Start with the larger number (72) and the smaller number (28).
72 and 28
Step 2: Divide the larger number by the smaller number and find the remainder.
72 ÷ 28 = 2 with a remainder of 16
Step 3: Replace the larger number with the smaller number, and the smaller number with the remainder.
28 and 16
Step 4: Repeat steps 2 and 3 until the remainder is 0.
28 ÷ 16 = 1 with a remainder of 12 16 ÷ 12 = 1 with a remainder of 4 12 ÷ 4 = 3 with a remainder of 0
Step 5: The last non-zero remainder is the GCF.
The last non-zero remainder is 4, therefore, the GCF of 28 and 72 is 4.
Method 3: Listing Factors
This method is straightforward but can become cumbersome for larger numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Factors of 28: 1, 2, 4, 7, 14, 28
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
The common factors are 1, 2, and 4. The greatest common factor is 4.
Why is Finding the GCF Important? Real-World Applications
The seemingly simple task of finding the GCF has significant practical applications across various fields:
-
Fraction Simplification: Reducing fractions to their simplest form is crucial in mathematics and science. For example, the fraction 28/72 can be simplified to 7/18 by dividing both the numerator and denominator by their GCF (4). This simplification makes calculations easier and results clearer.
-
Measurement and Construction: Imagine you're tiling a floor with square tiles. If the room measures 28 feet by 72 feet, finding the GCF (4) allows you to determine the largest square tile (4 feet x 4 feet) that can be used without cutting any tiles. This minimizes waste and simplifies the tiling process.
-
Data Organization: In computer science, the GCF can be used to efficiently organize and manage data. For example, it can be applied in algorithms for data compression and efficient data storage.
-
Cryptography: The Euclidean Algorithm, used to find the GCF, is a fundamental building block in many cryptographic systems. It plays a crucial role in ensuring the security of digital communications and transactions.
-
Music Theory: The GCF can be used to determine the greatest common divisor of two musical intervals, which can help in understanding and analyzing musical harmony. This helps in composing and creating music with more pleasing sounds and patterns.
-
Scheduling: The GCF is relevant when figuring out when certain repeating events will occur simultaneously. For example, if one event repeats every 28 days and another repeats every 72 days, the GCF tells us how many days must pass before they both occur on the same day again (4 days).
Choosing the Right Method
The best method for finding the GCF depends on the numbers involved.
-
Prime Factorization: This is a good method for smaller numbers or when understanding the prime factorization is important.
-
Euclidean Algorithm: This is the most efficient method for larger numbers, especially when dealing with numbers that are difficult to factorize.
-
Listing Factors: This method is suitable for very small numbers, but it becomes impractical for larger numbers.
For the numbers 28 and 72, both the prime factorization and the Euclidean Algorithm are efficient. The listing factors method is the least efficient but useful for understanding the concept.
Conclusion
Finding the greatest common factor of 28 and 72, which is 4, is more than just a simple arithmetic exercise. It's a gateway to understanding fundamental concepts in number theory with far-reaching applications in various fields. Mastering the different methods for finding the GCF—prime factorization, the Euclidean algorithm, and listing factors—provides a strong foundation for tackling more complex mathematical problems and appreciating the elegance and utility of number theory in the real world. This understanding empowers you to solve problems more efficiently and creatively. The seemingly simple act of finding a GCF unlocks a world of mathematical possibilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 28 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.