What Is The Greatest Common Factor Of 44 And 66
News Co
Apr 02, 2025 · 6 min read
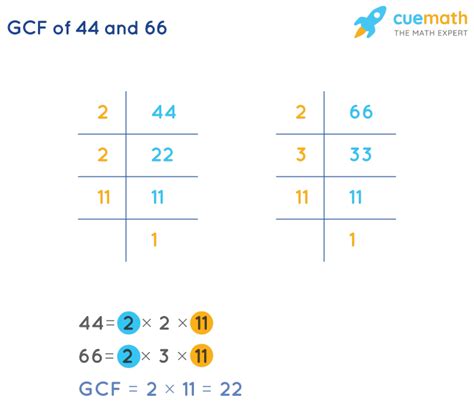
Table of Contents
What is the Greatest Common Factor of 44 and 66? A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic problem. However, understanding the underlying principles and exploring different methods for solving such problems unlocks a deeper appreciation of number theory and its applications in various fields like cryptography and computer science. This article will delve into the question: What is the greatest common factor of 44 and 66? and expand upon the concept of GCF in a comprehensive and engaging manner.
Understanding the Greatest Common Factor (GCF)
Before we tackle the specific problem of finding the GCF of 44 and 66, let's establish a firm understanding of what the GCF actually represents. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
For example, let's consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The largest of these common factors is 6, so the GCF of 12 and 18 is 6.
Methods for Finding the GCF
Several methods can be used to determine the GCF of two numbers. Let's explore three common approaches:
1. Listing Factors
This method, as illustrated in the example above, involves listing all the factors of each number and then identifying the largest factor common to both. While straightforward for smaller numbers, it becomes cumbersome and time-consuming for larger numbers. This method is best suited for introductory understanding and smaller numbers.
2. Prime Factorization
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors. The GCF is the product of these common prime factors, each raised to the lowest power that appears in either factorization.
Let's illustrate this with an example using 12 and 18:
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹. Therefore, the GCF of 12 and 18 is 2 x 3 = 6.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Alternatively, and more commonly used, the Euclidean algorithm uses successive division with remainder. The algorithm proceeds as follows:
- Divide the larger number by the smaller number and find the remainder.
- Replace the larger number with the smaller number and the smaller number with the remainder.
- Repeat steps 1 and 2 until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 44 and 66:
- Divide 66 by 44: 66 = 44 x 1 + 22
- Replace 66 with 44 and 44 with 22.
- Divide 44 by 22: 44 = 22 x 2 + 0
The last non-zero remainder is 22, so the GCF of 44 and 66 is 22.
Solving the Problem: GCF of 44 and 66
Now, let's apply the most efficient method, the Euclidean algorithm, to find the GCF of 44 and 66:
- 66 ÷ 44 = 1 with a remainder of 22
- 44 ÷ 22 = 2 with a remainder of 0
Therefore, the greatest common factor of 44 and 66 is 22.
Applications of GCF
The concept of GCF extends far beyond simple arithmetic exercises. It has significant applications in various fields:
-
Simplifying Fractions: The GCF is crucial in simplifying fractions to their lowest terms. By dividing both the numerator and the denominator by their GCF, we obtain an equivalent fraction in its simplest form. For example, the fraction 44/66 can be simplified to 2/3 by dividing both the numerator and the denominator by their GCF, 22.
-
Solving Word Problems: Many word problems in mathematics and other fields involve finding the GCF. For example, determining the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the floor's length and width.
-
Cryptography: The GCF plays a vital role in various cryptographic algorithms, such as the RSA algorithm, which is widely used for secure data transmission over the internet. The efficiency of GCF calculation directly impacts the speed and security of these algorithms.
-
Computer Science: The GCF is used in computer algorithms for tasks like simplifying expressions, optimizing code, and managing data structures.
Beyond Two Numbers: Finding the GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and identify the common prime factors raised to their lowest powers. For the Euclidean algorithm, you would iteratively find the GCF of pairs of numbers until you have the GCF of all the numbers.
For example, to find the GCF of 12, 18, and 24:
- Prime factorization:
- 12 = 2² x 3
- 18 = 2 x 3²
- 24 = 2³ x 3
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCF of 12, 18, and 24 is 2 x 3 = 6.
Conclusion
Finding the greatest common factor of 44 and 66, which is 22, is a seemingly straightforward problem. However, exploring the various methods for calculating the GCF, such as listing factors, prime factorization, and the Euclidean algorithm, provides a deeper understanding of number theory and its broad applications across diverse fields. The Euclidean algorithm stands out as the most efficient method, particularly for larger numbers. Understanding the GCF is fundamental not only for simplifying fractions and solving mathematical problems but also for comprehending the complexities of cryptography and computer science algorithms. This comprehensive understanding enables us to approach more advanced mathematical concepts with confidence and appreciate the elegance and power of number theory.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 44 And 66 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.