What Is The Greatest Common Factor Of 45 And 30
News Co
Apr 04, 2025 · 5 min read
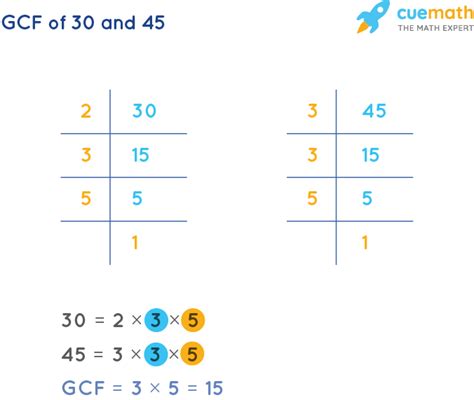
Table of Contents
What is the Greatest Common Factor of 45 and 30? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the concept opens doors to more complex mathematical concepts and has practical applications across various fields. This article delves into the GCF of 45 and 30, exploring multiple methods for calculation, explaining the underlying mathematical principles, and showcasing its relevance in real-world scenarios.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. Understanding the GCF is fundamental to simplifying fractions, solving algebraic equations, and working with various mathematical structures.
Why is the GCF Important?
The GCF plays a crucial role in various mathematical operations and real-world applications. Here are some key reasons for its importance:
-
Simplifying Fractions: Finding the GCF allows us to reduce fractions to their simplest form. For instance, if we have the fraction 30/45, finding the GCF helps us simplify it to its equivalent fraction in lowest terms.
-
Solving Algebraic Equations: The GCF is frequently used when factoring polynomials, a critical step in solving many algebraic equations.
-
Geometry and Measurement: The GCF is relevant in problems involving area, perimeter, and volume calculations, particularly when dealing with shapes that share common dimensions.
-
Number Theory: The GCF forms a cornerstone of number theory, a branch of mathematics dealing with the properties and relationships of numbers.
Methods for Finding the GCF of 45 and 30
Several methods exist for determining the greatest common factor of two numbers. Let's explore three common techniques:
1. Listing Factors Method
This is a straightforward approach, especially for smaller numbers. We list all the factors of each number and identify the largest common factor.
Factors of 45: 1, 3, 5, 9, 15, 45 Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
Comparing the lists, we see that the common factors are 1, 3, 5, and 15. The greatest common factor is 15.
2. Prime Factorization Method
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
Prime factorization of 45: 3² x 5 Prime factorization of 30: 2 x 3 x 5
The common prime factors are 3 and 5. The lowest power of 3 is 3¹ and the lowest power of 5 is 5¹. Therefore, the GCF is 3 x 5 = 15.
3. Euclidean Algorithm
This is a highly efficient algorithm, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, which represents the GCF.
Let's apply the Euclidean Algorithm to 45 and 30:
- 45 = 1 x 30 + 15
- 30 = 2 x 15 + 0
Since the remainder is 0, the GCF is the last non-zero remainder, which is 15.
Applications of GCF in Real-World Scenarios
The GCF's applications extend beyond theoretical mathematics. Let's consider some practical examples:
1. Simplifying Fractions in Baking
Imagine you're baking a cake and the recipe calls for 30 grams of butter and 45 grams of flour. To simplify the ratio, you find the GCF of 30 and 45, which is 15. This allows you to express the ratio as 2:3 (30/15 : 45/15), simplifying your understanding of the ingredient proportions.
2. Dividing Resources Equally
Suppose you have 45 apples and 30 oranges, and you want to distribute them equally among several baskets so that each basket contains the same number of apples and oranges. The GCF (15) tells you that you can create 15 baskets, each with 3 apples and 2 oranges.
3. Arranging Objects in Arrays
If you have 45 square tiles and you want to arrange them in a rectangular array where both dimensions are whole numbers, the factors of 45 will give you the possible dimensions. If you also have 30 triangular tiles and want to arrange both types of tiles in similar sized arrays, the common factors, especially the greatest common factor, will be crucial to determine the size of the arrays.
Beyond the Basics: Exploring Further Concepts
The GCF forms the foundation for understanding more advanced mathematical concepts:
1. Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive integer that is divisible by both numbers. The GCF and LCM are related by the formula: LCM(a, b) x GCF(a, b) = a x b. For 45 and 30, the LCM is 90. This relationship is vital in various mathematical problems, especially those involving fractions and rational expressions.
2. Modular Arithmetic
Modular arithmetic, a system of arithmetic for integers, uses the concept of congruence modulo n. The GCF plays a critical role in determining whether a solution exists in such systems.
3. Diophantine Equations
These equations involve finding integer solutions to algebraic equations. The GCF often assists in determining whether a solution exists and, if so, finding the solution(s).
4. Abstract Algebra
The GCF concept extends to abstract algebra, particularly in the study of rings and ideals, where the concept of a greatest common divisor is generalized.
Conclusion
Determining the greatest common factor of 45 and 30, while seemingly elementary, provides a gateway to a vast landscape of mathematical principles and applications. Understanding different methods for finding the GCF not only improves computational skills but also enhances problem-solving abilities across various fields. From simplifying recipes to solving complex algebraic equations, the GCF's utility extends far beyond the realm of textbook exercises, illustrating its fundamental importance in mathematics and its relevance in our everyday lives. The exploration of the GCF doesn't merely provide an answer (15) but, rather, unlocks a deeper understanding of the intricate workings of numbers and their relationships.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 45 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.