What Is The Greatest Common Factor Of 4xy2 And 20x2y4
News Co
Mar 17, 2025 · 5 min read
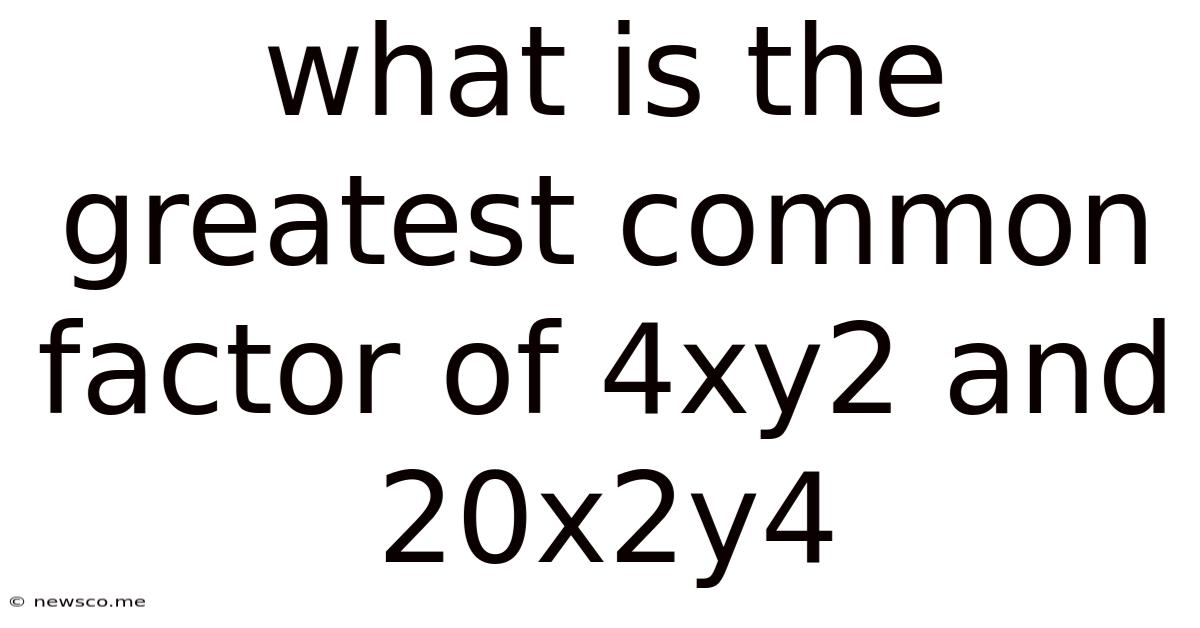
Table of Contents
What is the Greatest Common Factor of 4xy² and 20x²y⁴? A Deep Dive into Finding GCFs
Finding the greatest common factor (GCF) is a fundamental concept in mathematics, particularly in algebra. Understanding how to determine the GCF is crucial for simplifying expressions, solving equations, and working with fractions. This article will thoroughly explore how to find the GCF of 4xy² and 20x²y⁴, providing a step-by-step explanation and expanding upon the broader context of GCFs. We'll also delve into various methods and explore real-world applications.
Understanding Greatest Common Factors (GCFs)
The greatest common factor, or GCF, of two or more numbers or algebraic expressions is the largest number or expression that divides evenly into all of them without leaving a remainder. Think of it as the largest building block that is common to all the numbers or expressions. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides evenly into both 12 and 18.
When working with algebraic expressions like 4xy² and 20x²y⁴, the process is similar but involves considering both numerical coefficients and variables.
Finding the GCF of 4xy² and 20x²y⁴: A Step-by-Step Guide
Let's break down the process of finding the GCF of 4xy² and 20x²y⁴. We'll approach this using two common methods:
Method 1: Prime Factorization
This method involves breaking down each term into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, etc.).
-
Prime Factorization of 4xy²:
4xy² can be written as 2 x 2 x x x y x y (2²xy²)
-
Prime Factorization of 20x²y⁴:
20x²y⁴ can be written as 2 x 2 x 5 x x x y x y x y x y (2² x 5 x x²y⁴)
-
Identify Common Factors:
Now, we identify the common prime factors in both expressions:
- Two factors of 2 (2²)
- One factor of x (x)
- Two factors of y (y²)
-
Multiply the Common Factors:
To find the GCF, we multiply the common prime factors together:
2 x 2 x x x y x y = 4xy²
Therefore, the greatest common factor of 4xy² and 20x²y⁴ is 4xy².
Method 2: Listing Factors
This method involves listing all the factors of each term and then identifying the largest common factor. While effective for smaller numbers, it can become cumbersome with larger numbers or algebraic expressions.
-
Factors of 4xy²: 1, 2, 4, x, y, 2x, 2y, 4x, 4y, xy, 2xy, 4xy, xy², 2xy², 4xy²
-
Factors of 20x²y⁴: 1, 2, 4, 5, 10, 20, x, y, 2x, 2y, 4x, 4y, 5x, 5y, 10x, 10y, 20x, 20y, x², xy, 2x², 2xy, 4x², 4xy, 5x², 5xy, 10x², 10xy, 20x², 20xy, x²y, 2x²y, 4x²y, 5x²y, 10x²y, 20x²y, xy², 2xy², 4xy², 5xy², 10xy², 20xy², x²y², 2x²y², 4x²y², 5x²y², 10x²y², 20x²y², xy³, 2xy³, 4xy³, 5xy³, 10xy³, 20xy³, x²y³, 2x²y³, 4x²y³, 5x²y³, 10x²y³, 20x²y³, xy⁴, 2xy⁴, 4xy⁴, 5xy⁴, 10xy⁴, 20xy⁴, x²y⁴, 2x²y⁴, 4x²y⁴, 5x²y⁴, 10x²y⁴, 20x²y⁴
-
Identify the Largest Common Factor:
By comparing the two lists, we can see that the largest common factor is 4xy².
Simplifying Algebraic Expressions Using GCF
The GCF plays a crucial role in simplifying algebraic expressions. Consider the expression 4xy² + 20x²y⁴. Since the GCF of these two terms is 4xy², we can factor it out:
4xy² + 20x²y⁴ = 4xy²(1 + 5xy²)
This simplified form is often easier to work with when solving equations or performing other algebraic manipulations.
Applications of GCFs in Real-World Scenarios
While the concept of GCF might seem purely mathematical, it has practical applications in various real-world situations:
-
Dividing Resources: Imagine you have 12 apples and 18 oranges, and you want to divide them equally among several people without any leftovers. Finding the GCF (6) tells you that you can divide the fruit among 6 people.
-
Geometry Problems: GCFs are used in solving geometric problems involving area and perimeter calculations. For instance, determining the side length of the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the length and width of the floor.
-
Construction and Design: In construction and design, GCFs are helpful in determining the most efficient way to cut materials or arrange objects.
-
Manufacturing and Packaging: Packaging products efficiently often involves using the GCF to determine the optimal dimensions for boxes or containers to minimize waste and maximize capacity.
Further Exploration of GCFs: Beyond Two Terms
The methods discussed above can be extended to finding the GCF of more than two terms. For example, if you need to find the GCF of 6x²y³, 12x³y², and 18x⁴y, you would follow similar steps:
- Find the prime factorization of each term.
- Identify the common prime factors.
- Multiply the common factors to find the GCF.
In this case, the GCF would be 6x²y.
Conclusion: Mastering the GCF for Mathematical Success
Understanding and mastering the concept of greatest common factor is fundamental to success in algebra and beyond. Whether you're simplifying expressions, solving equations, or tackling real-world problems, the ability to efficiently find the GCF is an invaluable skill. This article has provided a comprehensive guide, covering various methods and highlighting the practical applications of this important mathematical concept. By understanding the underlying principles and practicing the techniques outlined here, you can confidently tackle GCF problems of varying complexity. Remember to always break down the terms into their prime factors, ensuring a thorough and accurate determination of the GCF. This will lay a solid foundation for more advanced mathematical concepts and problem-solving.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 4xy2 And 20x2y4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.