What Is The Greatest Common Factor Of 51 And 85
News Co
Mar 17, 2025 · 5 min read
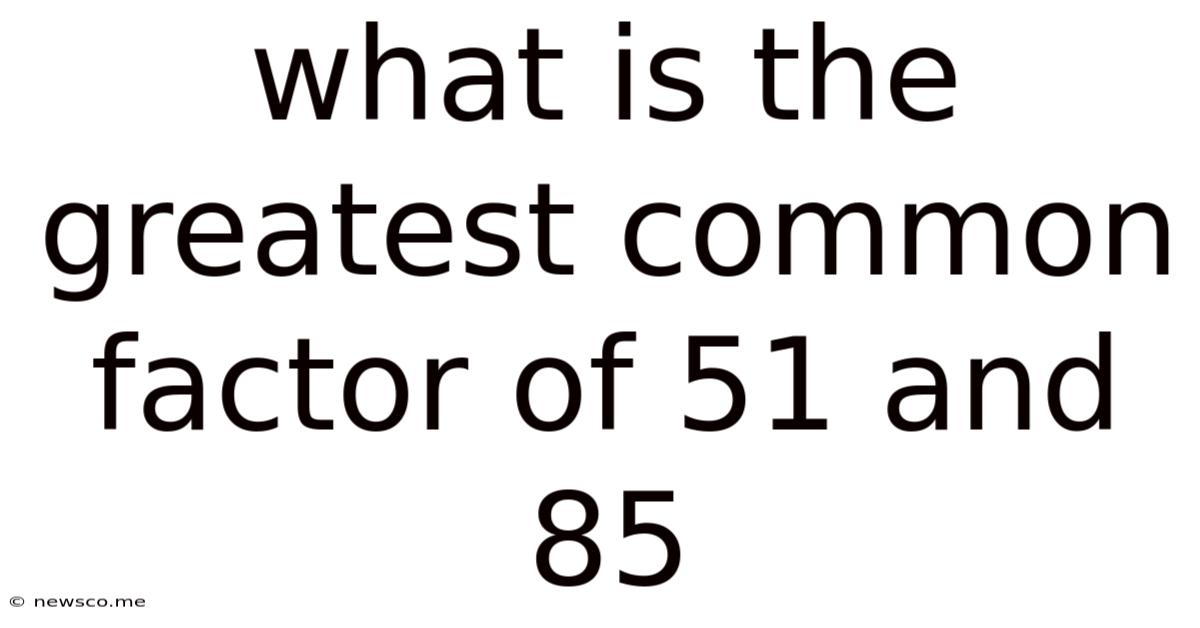
Table of Contents
What is the Greatest Common Factor of 51 and 85? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but it's a fundamental concept in number theory with wide-ranging applications in mathematics and computer science. This article will explore the GCF of 51 and 85 in detail, examining various methods to calculate it and highlighting the underlying mathematical principles. We'll also delve into the broader significance of GCFs and their practical uses.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Understanding GCFs is crucial for simplifying fractions, solving algebraic equations, and understanding various mathematical structures. It's a building block for more advanced concepts in number theory and abstract algebra.
Methods for Finding the GCF of 51 and 85
Several methods can be used to determine the greatest common factor of 51 and 85. Let's explore the most common approaches:
1. Listing Factors
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 51: 1, 3, 17, 51 Factors of 85: 1, 5, 17, 85
Comparing the two lists, we see that the common factors are 1 and 17. Therefore, the greatest common factor of 51 and 85 is 17.
2. Prime Factorization
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
Prime factorization of 51: 3 x 17 Prime factorization of 85: 5 x 17
The only common prime factor is 17. Therefore, the GCF of 51 and 85 is 17.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 51 and 85:
- 85 = 51 x 1 + 34
- 51 = 34 x 1 + 17
- 34 = 17 x 2 + 0
The last non-zero remainder is 17, so the GCF of 51 and 85 is 17.
The Significance of the GCF of 51 and 85
The fact that the GCF of 51 and 85 is 17 is not just a numerical result; it has several implications:
-
Simplifying Fractions: If you have a fraction with 51 as the numerator and 85 as the denominator (51/85), you can simplify it by dividing both the numerator and denominator by their GCF, which is 17. This simplifies the fraction to 3/5.
-
Algebraic Applications: GCFs are essential in simplifying algebraic expressions. For instance, if you have the expression 51x + 85y, you can factor out the GCF (17) to get 17(3x + 5y). This simplification is crucial in solving equations and simplifying complex algebraic manipulations.
-
Number Theory Concepts: The concept of GCF is fundamental to various number theory concepts, such as relatively prime numbers (numbers with a GCF of 1) and modular arithmetic. Understanding GCFs is a stepping stone to exploring more advanced topics in number theory.
-
Computer Science Applications: The Euclidean algorithm, used to find the GCF, is a highly efficient algorithm with applications in cryptography and computer science. It's used in various cryptographic protocols and algorithms for ensuring data security.
Relatively Prime Numbers and Coprime Numbers
Two numbers are considered relatively prime or coprime if their greatest common factor is 1. While 51 and 85 are not relatively prime (their GCF is 17), understanding this concept is vital in number theory. Many mathematical properties and theorems rely on the concept of relatively prime numbers.
For example, if two numbers are relatively prime, they share no common divisors other than 1. This property has significant implications in various mathematical fields, including cryptography, where the security of certain encryption algorithms relies on the difficulty of finding large prime numbers and ensuring they are relatively prime.
Applications of GCF in Real-World Scenarios
Beyond the theoretical realm, GCFs have practical applications in various real-world scenarios:
-
Dividing Objects: Imagine you have 51 apples and 85 oranges, and you want to divide them into identical groups with the largest possible number of items in each group. The GCF (17) tells you that you can create 17 groups, each containing 3 apples and 5 oranges.
-
Project Management: In project management, determining the GCF can help in optimizing resource allocation. If a project requires 51 hours of work from one team and 85 hours from another, finding the GCF allows for the most efficient scheduling and resource utilization.
-
Geometric Problems: GCFs play a role in solving geometric problems involving the dimensions of objects. For instance, determining the largest square tile that can perfectly cover a rectangular area with dimensions of 51 units and 85 units would involve finding the GCF of 51 and 85.
Conclusion: The Power of the GCF
Finding the greatest common factor of 51 and 85, which is 17, is more than just a simple arithmetic exercise. It's a gateway to understanding fundamental concepts in number theory, with significant applications in various fields, from simplifying fractions to securing cryptographic systems. The different methods presented – listing factors, prime factorization, and the Euclidean algorithm – showcase the versatility and efficiency of mathematical techniques. Understanding GCFs empowers us to approach mathematical problems systematically and efficiently, highlighting the inherent power and elegance of mathematics. This deep dive into the GCF of 51 and 85 showcases its multifaceted importance and relevance across numerous mathematical and practical domains. Mastering this concept is essential for anyone interested in further exploring the fascinating world of numbers and their intricate relationships.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 51 And 85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.