What Is The Greatest Common Factor Of 8 And 40
News Co
Mar 20, 2025 · 5 min read
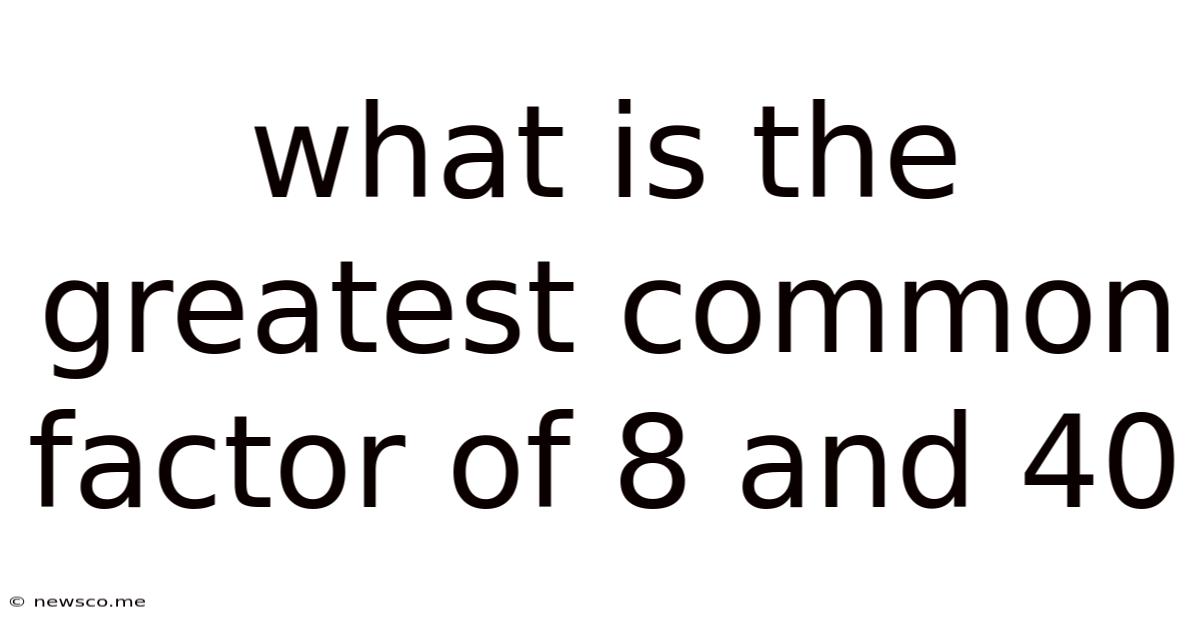
Table of Contents
What is the Greatest Common Factor of 8 and 40? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but it unlocks a deeper understanding of number theory and has practical applications in various fields. This article will explore the concept of GCF, demonstrate multiple methods for finding the GCF of 8 and 40, and delve into the broader significance of this fundamental concept in mathematics.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. Understanding the GCF is crucial in simplifying fractions, solving algebraic equations, and various other mathematical operations.
Why is the GCF Important?
The GCF is more than just a mathematical curiosity. Its applications extend across numerous areas:
-
Simplifying Fractions: The GCF allows you to reduce fractions to their simplest form. For instance, the fraction 40/8 can be simplified using the GCF to 5/1.
-
Algebraic Simplification: GCF plays a vital role in factoring algebraic expressions, making them easier to solve and manipulate.
-
Geometry and Measurement: GCF is used in problems related to finding the dimensions of the largest square that can tile a given rectangle, or determining the common measure for units.
-
Cryptography: While seemingly unrelated, the concept of GCF underpins some fundamental aspects of cryptography, particularly in the Euclidean algorithm used for key generation and decryption.
Methods for Finding the GCF of 8 and 40
Several methods exist for determining the GCF of two numbers. We'll explore three common approaches: listing factors, prime factorization, and the Euclidean algorithm.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and identify the largest common factor.
Factors of 8: 1, 2, 4, 8 Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
By comparing the two lists, we see that the common factors are 1, 2, 4, and 8. The greatest of these common factors is 8. Therefore, the GCF of 8 and 40 is 8.
This method becomes less efficient when dealing with larger numbers, as listing all factors can be time-consuming.
Method 2: Prime Factorization
Prime factorization involves expressing each number as a product of its prime factors. The GCF is then found by identifying the common prime factors raised to the lowest power.
Prime factorization of 8: 2 x 2 x 2 = 2³ Prime factorization of 40: 2 x 2 x 2 x 5 = 2³ x 5
Both numbers share three factors of 2. Therefore, the GCF is 2³ = 8.
This method is more efficient than listing factors, particularly for larger numbers, as it focuses on prime numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger integers. It uses the principle of repeated division with remainder.
The steps are as follows:
- Divide the larger number (40) by the smaller number (8): 40 ÷ 8 = 5 with a remainder of 0.
Since the remainder is 0, the smaller number (8) is the GCF.
If the remainder were not 0, we would continue the process:
- Divide the previous divisor (8) by the remainder.
- Repeat until the remainder is 0. The last non-zero remainder is the GCF.
This method is highly efficient for large numbers and forms the basis of many computer algorithms for GCF calculation.
Expanding on the Concept of GCF
The concept of GCF extends beyond just two numbers. We can find the GCF of three or more numbers using any of the methods described above. For instance, to find the GCF of 8, 40, and 24:
Prime Factorization Method:
- 8 = 2³
- 40 = 2³ x 5
- 24 = 2³ x 3
The common prime factor is 2³, so the GCF of 8, 40, and 24 is 8.
Applications of GCF in Real-World Scenarios
While the concept may seem abstract, the GCF has numerous real-world applications:
-
Baking: If you have 8 cups of flour and 40 cups of sugar, and a recipe requires the same amount of flour and sugar, the GCF (8) determines the number of times you can perfectly make the recipe before running out of one ingredient.
-
Construction: Imagine you need to divide a rectangular area into identical squares. The dimensions of the largest possible square (the side length) are determined by the GCF of the rectangle's length and width.
-
Software Development: Algorithms related to GCF are used in various computer programs, such as those dealing with data compression, image processing, and cryptography.
-
Music Theory: The GCF plays a role in determining the harmonic relationships between musical notes.
Beyond the Basics: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM of two or more numbers is the smallest positive integer that is a multiple of all the numbers. The relationship between GCF and LCM is:
LCM(a, b) * GCF(a, b) = a * b
Knowing this relationship allows you to quickly calculate the LCM if you already know the GCF (and vice versa). For 8 and 40:
GCF(8, 40) = 8 LCM(8, 40) = (8 * 40) / 8 = 40
Conclusion: The Power of Simple Concepts
The seemingly simple concept of the greatest common factor holds significant power and practical utility. Understanding different methods for calculating the GCF, from listing factors to utilizing the Euclidean algorithm, allows us to tackle problems efficiently, whether it's simplifying fractions, factoring algebraic expressions, or solving real-world problems related to measurement, division, or even music. The GCF is a fundamental building block in number theory, highlighting the elegance and interconnectedness of mathematical concepts. Its importance extends far beyond simple arithmetic, illustrating how seemingly basic concepts underpin advanced mathematical and computational applications. Mastering the GCF not only enhances mathematical skills but also provides a valuable foundation for further exploration in number theory and its various applications.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 8 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.