What Is The Highest Common Factor Of 18 And 27
News Co
Mar 28, 2025 · 5 min read
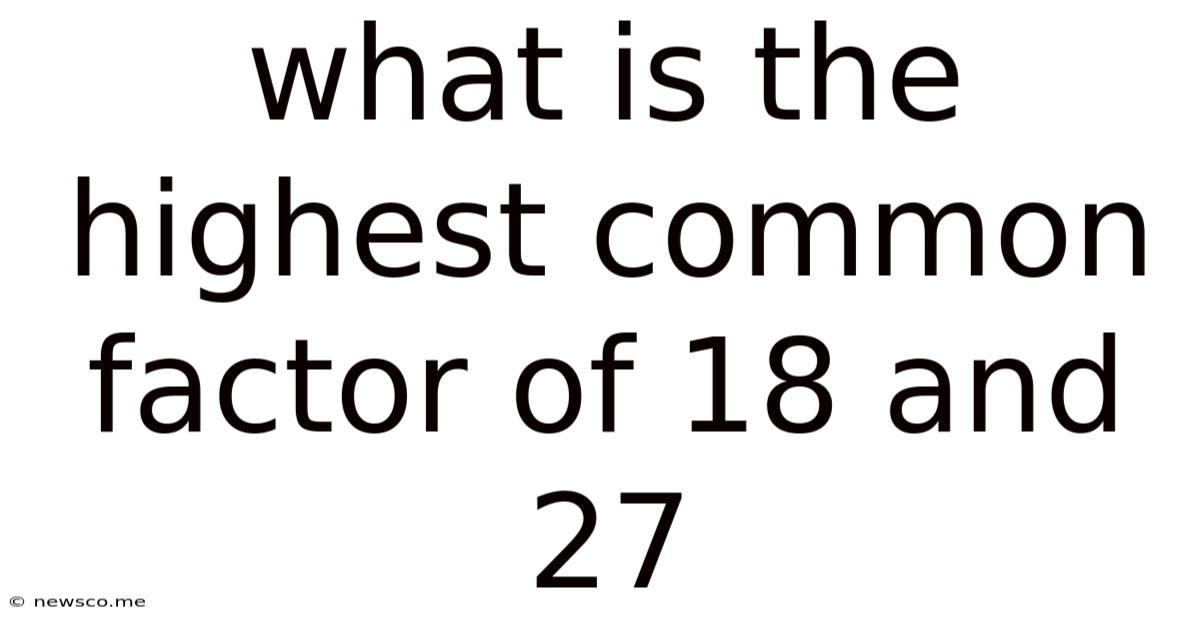
Table of Contents
What is the Highest Common Factor (HCF) of 18 and 27? A Deep Dive into Number Theory
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with applications extending far beyond basic arithmetic. This article will explore how to determine the HCF of 18 and 27, utilizing several methods, and then delve deeper into the broader implications and applications of this mathematical concept.
Understanding the Highest Common Factor (HCF)
Before we tackle the specific problem of finding the HCF of 18 and 27, let's define the term precisely. The highest common factor (HCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The highest of these common factors is 6, so the HCF of 12 and 18 is 6.
Method 1: Prime Factorization
The prime factorization method is a reliable and systematic way to find the HCF of any two numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
1. Find the prime factorization of 18:
18 = 2 x 3 x 3 = 2 x 3²
2. Find the prime factorization of 27:
27 = 3 x 3 x 3 = 3³
3. Identify common prime factors:
Both 18 and 27 share the prime factor 3.
4. Determine the HCF:
The lowest power of the common prime factor(s) is the HCF. In this case, the lowest power of 3 is 3², which is 9.
Therefore, the HCF of 18 and 27 is 9.
Method 2: Listing Factors
This method, while straightforward for smaller numbers, becomes less efficient with larger numbers. It involves listing all the factors of each number and identifying the largest common factor.
1. List the factors of 18: 1, 2, 3, 6, 9, 18
2. List the factors of 27: 1, 3, 9, 27
3. Identify common factors: 1, 3, 9
4. Determine the HCF: The largest common factor is 9.
Therefore, the HCF of 18 and 27 is 9.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, especially useful for larger numbers where prime factorization might become cumbersome. This algorithm is based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, at which point that number is the HCF.
1. Start with the larger number (27) and the smaller number (18):
27 ÷ 18 = 1 with a remainder of 9
2. Replace the larger number with the remainder:
Now we find the HCF of 18 and 9.
18 ÷ 9 = 2 with a remainder of 0
3. Since the remainder is 0, the HCF is the last non-zero remainder.
Therefore, the HCF of 18 and 27 is 9.
Applications of the Highest Common Factor
The concept of HCF extends far beyond simple arithmetic exercises. It has significant applications in various fields, including:
1. Fraction Simplification:
HCF is crucial for simplifying fractions to their lowest terms. By dividing both the numerator and denominator by their HCF, we obtain an equivalent fraction in its simplest form. For example, the fraction 18/27 can be simplified to 2/3 by dividing both the numerator and denominator by their HCF, which is 9.
2. Measurement and Division Problems:
HCF finds practical application in scenarios involving measurement and division. For instance, if you have two pieces of wood, one 18 inches long and the other 27 inches long, and you want to cut them into pieces of equal length without any waste, the longest possible length of each piece would be the HCF of 18 and 27, which is 9 inches.
3. Cryptography and Number Theory:
HCF plays a vital role in cryptography, particularly in algorithms like the RSA algorithm, which relies on the properties of prime numbers and their greatest common divisors for secure data encryption and decryption.
4. Computer Science and Algorithm Design:
The Euclidean algorithm for finding the HCF is a fundamental algorithm in computer science, used in various applications, including simplifying fractions within computer programs and in tasks involving modular arithmetic. The efficiency of the Euclidean algorithm makes it particularly valuable in situations requiring rapid computation of HCFs.
5. Music Theory:
Surprisingly, HCF also finds its place in music theory. When determining the greatest common divisor of two musical intervals, the HCF can be utilized to simplify interval relationships and understand harmonic structures more effectively.
Conclusion: Beyond the Numbers
Determining the highest common factor of 18 and 27, as demonstrated above, is a relatively straightforward task. However, the underlying concept and its various applications reveal the HCF's profound importance in various fields of mathematics, science, and even music. Understanding the HCF provides a foundation for tackling more complex mathematical problems and offers a glimpse into the interconnectedness of mathematical concepts. Whether you're simplifying fractions, solving measurement problems, or exploring more advanced mathematical concepts, mastering the HCF is a valuable skill with far-reaching implications. The various methods presented here – prime factorization, listing factors, and the Euclidean algorithm – each offer a distinct approach to solving the problem, illustrating the versatility and elegance of mathematical problem-solving. The choice of method often depends on the size of the numbers involved and the computational resources available. Regardless of the chosen approach, understanding the concept of the HCF and its applications is a crucial step in developing a deeper understanding of number theory and its practical applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Highest Common Factor Of 18 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.