What Is The Integral Of 2x
News Co
Mar 21, 2025 · 5 min read
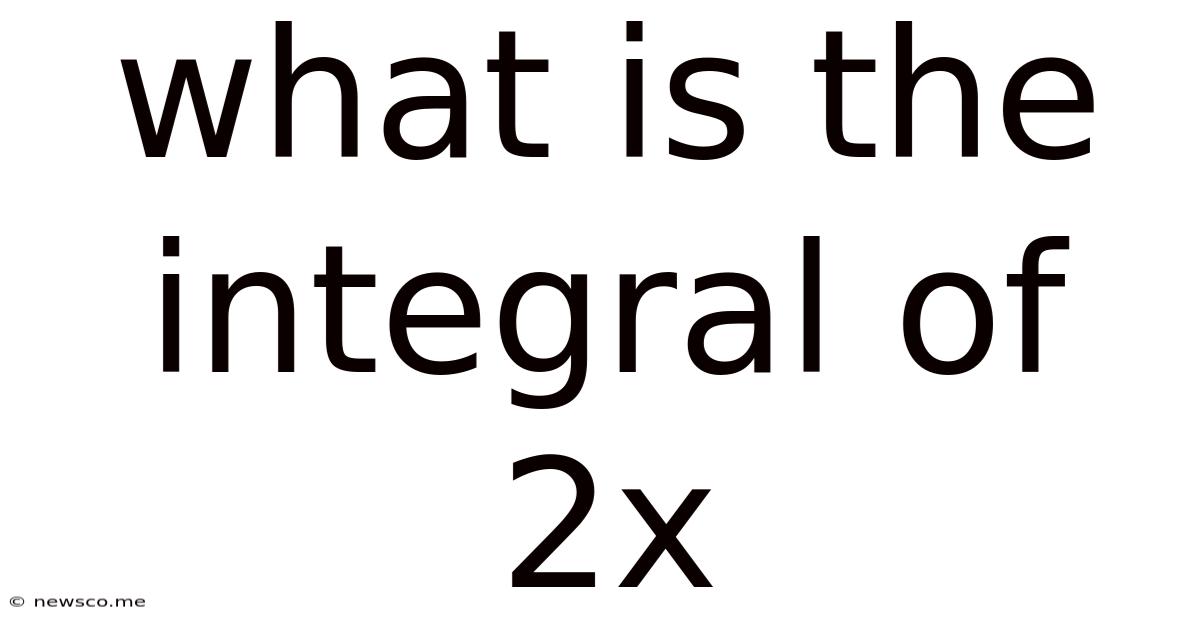
Table of Contents
What is the Integral of 2x? A Comprehensive Guide
The seemingly simple question, "What is the integral of 2x?" opens the door to a fascinating exploration of integral calculus, a cornerstone of mathematics with far-reaching applications in science, engineering, and beyond. This comprehensive guide will not only answer that question directly but also delve into the underlying concepts, methods, and practical implications of integration.
Understanding Integrals: The Reverse of Differentiation
Before tackling the integral of 2x, it's crucial to understand the fundamental relationship between integration and differentiation. Differentiation finds the instantaneous rate of change of a function, while integration finds the function whose derivative is the given function. In simpler terms, integration is the reverse process of differentiation.
Think of it like this: if differentiation is finding the slope of a curve at a specific point, integration is finding the area under that curve. This area interpretation is crucial for understanding the applications of integrals.
The Power Rule of Integration
The integral of 2x can be solved using the power rule of integration, a fundamental tool for finding the indefinite integral of polynomial functions. The power rule states:
∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C
where:
- ∫ represents the integral sign.
- xⁿ is the function being integrated.
- dx indicates that the integration is with respect to x.
- n is any real number except -1.
- C is the constant of integration. This is crucial because the derivative of a constant is always zero, meaning that infinitely many functions could have the same derivative.
Solving the Integral of 2x
Now, let's apply the power rule to find the integral of 2x. We can rewrite 2x as 2x¹. Here, n = 1. Applying the power rule:
∫2x¹ dx = 2 ∫x¹ dx = 2 * [(x¹⁺¹)/(1+1)] + C = 2 * (x²)/2 + C = x² + C
Therefore, the integral of 2x is x² + C.
The Significance of the Constant of Integration (C)
The constant of integration, C, is a critical component of indefinite integrals. It represents an arbitrary constant that can take on any real value. Why is it important? Because the derivative of any constant is zero. If we differentiate x² + C, we get 2x, regardless of the value of C.
This means there's a family of functions, each differing only by a vertical shift, that all share the same derivative, 2x. The constant C accounts for this family of solutions.
Visualizing the Integral: The Area Under the Curve
Let's visualize the integral of 2x graphically. The function y = 2x represents a straight line with a slope of 2. The integral, x² + C, represents a family of parabolas. Each parabola corresponds to a different value of C, resulting in a vertical shift along the y-axis.
The definite integral of 2x from a to b, represented as:
∫[a, b] 2x dx
represents the signed area under the curve y = 2x, between the limits a and b. The term "signed" indicates that areas below the x-axis are considered negative.
Definite Integrals vs. Indefinite Integrals
We've discussed indefinite integrals, which result in a family of functions. Definite integrals, on the other hand, provide a numerical value representing the area under the curve between specified limits. To calculate a definite integral, we first find the indefinite integral and then evaluate it at the upper and lower limits, subtracting the result at the lower limit from the result at the upper limit.
For example, to find the definite integral of 2x from 1 to 3:
∫[1, 3] 2x dx = [x²]³₁ = (3)² - (1)² = 9 - 1 = 8
This means the area under the curve y = 2x, between x = 1 and x = 3, is 8 square units.
Applications of Integration: Real-World Examples
The integral of 2x, while seemingly simple, has many real-world applications. These applications extend far beyond simple area calculations. Here are a few examples:
1. Physics: Calculating Velocity and Displacement
In physics, the integral of acceleration with respect to time gives velocity, and the integral of velocity with respect to time gives displacement. If acceleration is a constant, say 2 m/s², then the integral of 2t (where t is time) gives the velocity function. This is directly analogous to our integral of 2x.
2. Engineering: Determining Areas and Volumes
Engineers frequently use integration to calculate areas of irregular shapes and volumes of complex objects. This is crucial in structural design, fluid mechanics, and many other fields.
3. Economics: Calculating Total Cost and Revenue
In economics, the integral of marginal cost (the cost of producing one more unit) gives the total cost function. Similarly, the integral of marginal revenue gives the total revenue function.
4. Statistics: Finding Probabilities
In statistics, integration is used extensively to calculate probabilities related to continuous random variables. The area under the probability density function represents the probability of a random variable falling within a specific range.
5. Computer Graphics: Rendering Curves and Surfaces
Integration plays a critical role in computer graphics, particularly in rendering smooth curves and surfaces. Algorithms used in 3D modeling often rely on integration techniques.
Advanced Integration Techniques
While the power rule is sufficient for integrating simple polynomial functions like 2x, more advanced techniques are needed for integrating more complex functions. These include:
-
Integration by Substitution (u-Substitution): This technique simplifies integrals by substituting a new variable, u, for a part of the integrand.
-
Integration by Parts: This technique is used to integrate products of functions. It's based on the product rule of differentiation.
-
Partial Fraction Decomposition: This method is used to integrate rational functions (fractions of polynomials).
-
Trigonometric Substitution: This technique involves substituting trigonometric functions to simplify integrals containing expressions involving square roots.
Conclusion: Mastering the Integral of 2x and Beyond
Understanding the integral of 2x is a crucial stepping stone in mastering integral calculus. The seemingly straightforward solution, x² + C, unlocks a world of powerful applications across various scientific and engineering disciplines. By grasping the fundamental concepts of integration, the power rule, the significance of the constant of integration, and the distinction between definite and indefinite integrals, you gain a strong foundation for tackling more complex integration problems and unlocking the full potential of this essential mathematical tool. Remember, consistent practice and exploration of advanced integration techniques are key to building expertise in this vital area of mathematics. The journey from understanding the integral of 2x to mastering advanced integration techniques is a rewarding one, opening doors to a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Integral Of 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.