What Is The Lcm Of 12 8
News Co
Mar 15, 2025 · 5 min read
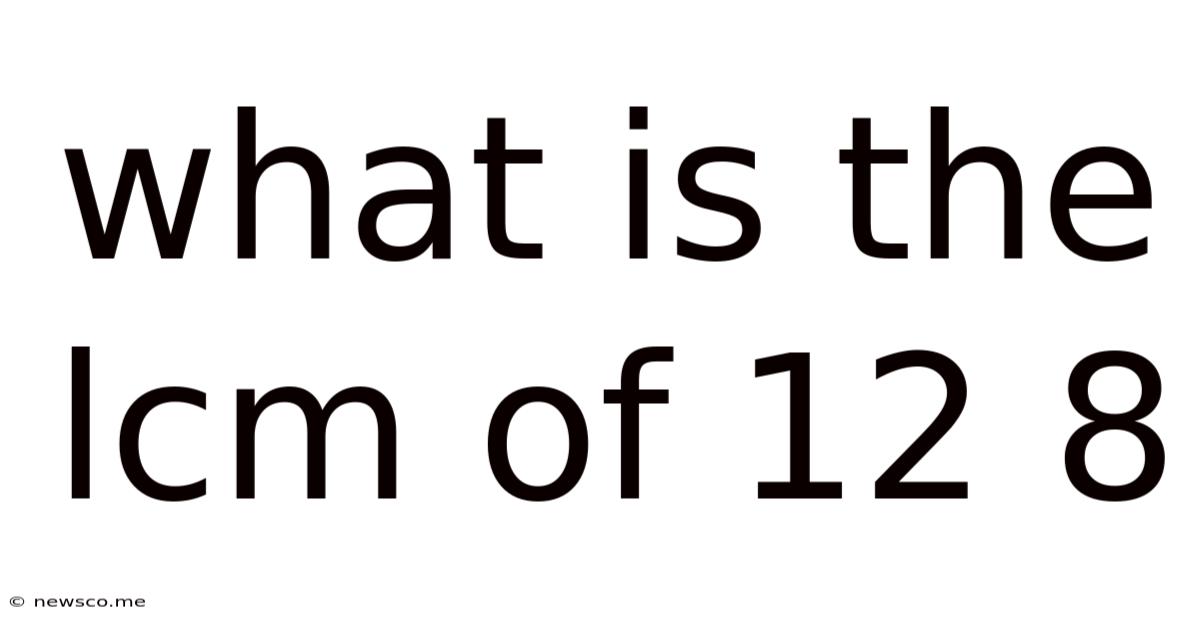
Table of Contents
What is the LCM of 12 and 8? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in various fields like fractions, scheduling, and even music theory. This article will explore the LCM of 12 and 8 in detail, explaining the process, different methods for calculation, and its significance within broader mathematical contexts. We'll also touch upon the practical applications of LCM and dispel some common misconceptions.
Understanding Least Common Multiples (LCM)
Before we delve into the specific case of 12 and 8, let's establish a solid understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, etc. The smallest common multiple is 6. Therefore, the LCM of 2 and 3 is 6.
Methods for Calculating the LCM of 12 and 8
Several methods exist to calculate the LCM of two or more numbers. We will explore the most common and efficient approaches, focusing on the LCM of 12 and 8.
1. Listing Multiples Method
This method involves listing the multiples of each number until you find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120…
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120…
By comparing the lists, we see that the smallest common multiple is 24. Therefore, the LCM of 12 and 8 is 24.
This method is straightforward for smaller numbers but can become cumbersome and time-consuming for larger numbers.
2. Prime Factorization Method
This method leverages the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM using prime factorization:
- Identify all the prime factors present in either number. In this case, we have 2 and 3.
- For each prime factor, take the highest power present in any of the factorizations. The highest power of 2 is 2³ (from 8), and the highest power of 3 is 3¹ (from 12).
- Multiply these highest powers together: 2³ x 3 = 8 x 3 = 24
Therefore, the LCM of 12 and 8 is 24, confirming our result from the listing multiples method. This method is generally more efficient for larger numbers than the listing multiples method.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship can be expressed as:
LCM(a, b) x GCD(a, b) = a x b
First, we find the GCD of 12 and 8. The divisors of 12 are 1, 2, 3, 4, 6, and 12. The divisors of 8 are 1, 2, 4, and 8. The greatest common divisor is 4.
Now, we can use the formula:
LCM(12, 8) x GCD(12, 8) = 12 x 8 LCM(12, 8) x 4 = 96 LCM(12, 8) = 96 / 4 = 24
This method provides an alternative approach, particularly useful when dealing with larger numbers where finding the GCD might be easier than directly finding the LCM.
Applications of LCM
The concept of LCM has numerous practical applications across various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires calculating the LCM of the denominators. For example, to add 1/8 and 1/12, we find the LCM of 8 and 12 (which is 24), and then express both fractions with a denominator of 24.
-
Scheduling Problems: LCM is useful in solving scheduling problems. For example, if two events occur at intervals of 12 and 8 days respectively, then the LCM (24) represents the number of days after which both events will occur on the same day again.
-
Music Theory: LCM plays a role in music theory, specifically in determining the least common multiple of the note durations, which is useful for calculating the overall duration of musical phrases.
-
Gear Ratios: In mechanics, LCM helps determine the gear ratios, allowing for the synchronized operation of multiple gears within a machine.
-
Tiling and Pattern Repetition: When arranging tiles or repeating patterns, calculating the LCM ensures seamless and consistent designs.
Common Misconceptions about LCM
-
LCM is always larger than the numbers involved: While it's usually the case, it's not a strict rule. If one number is a multiple of the other, the LCM is simply the larger number. For example, the LCM of 4 and 8 is 8.
-
LCM is only for two numbers: LCM can be calculated for any number of integers. The methods discussed can be extended to find the LCM of more than two numbers.
-
Confusing LCM with GCD: While related, LCM and GCD are distinct concepts. The LCM is the smallest common multiple, while the GCD is the greatest common divisor.
Conclusion
Determining the LCM of 12 and 8, which is 24, illustrates the fundamental importance of this concept in mathematics. Various methods exist for calculating the LCM, each with its own advantages and disadvantages depending on the context and magnitude of the numbers involved. The prime factorization method generally offers a more efficient approach for larger numbers. Understanding LCM is crucial for solving various problems across different disciplines, from basic arithmetic to advanced applications in engineering and music. By mastering this concept and understanding its applications, you can further enhance your mathematical skills and problem-solving capabilities.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 12 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.