What Is The Lcm Of 14 And 18
News Co
Apr 03, 2025 · 5 min read
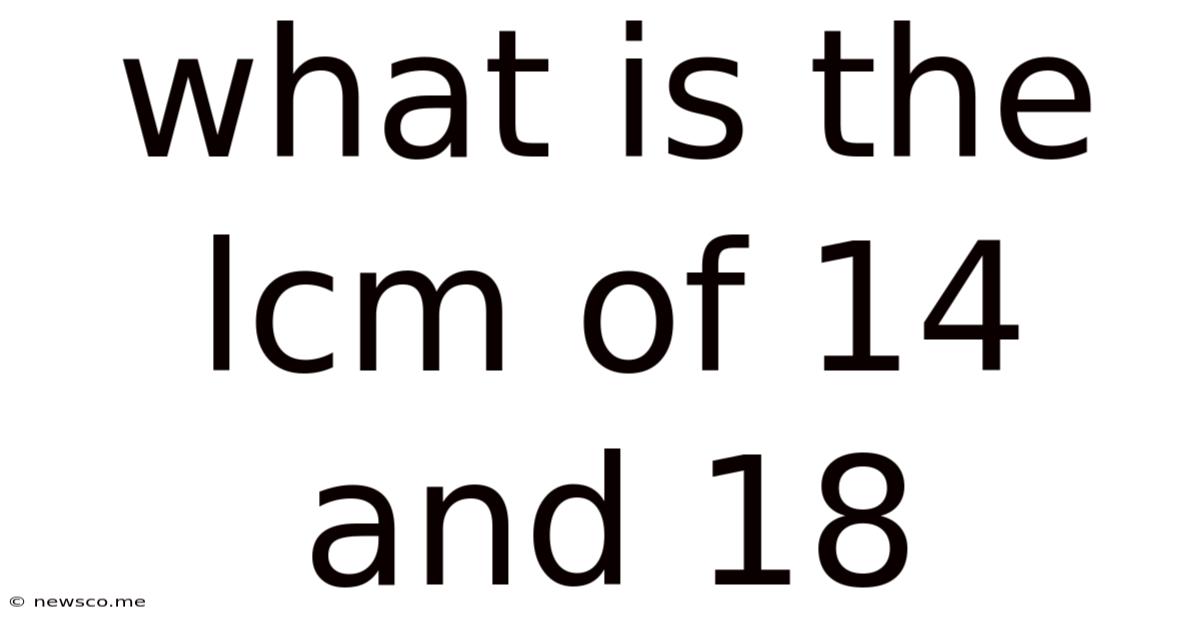
Table of Contents
What is the LCM of 14 and 18? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, with applications spanning various fields, from simple fraction addition to complex scheduling problems. This comprehensive guide will not only answer the question "What is the LCM of 14 and 18?" but will also explore the underlying principles, various methods for calculating LCMs, and real-world examples showcasing their practical utility.
Understanding Least Common Multiples (LCM)
Before we delve into the specifics of finding the LCM of 14 and 18, let's solidify our understanding of what an LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be evenly divided by all the given numbers without leaving a remainder.
Think of it like this: imagine you have two gears with different numbers of teeth (14 and 18 in our case). The LCM represents the number of rotations it takes for both gears to simultaneously return to their starting positions. This concept has practical applications in various fields, including:
- Scheduling: Determining when events that occur at different intervals will coincide.
- Fraction Operations: Finding a common denominator to add or subtract fractions.
- Music Theory: Calculating rhythmic patterns and harmonies.
- Engineering: Synchronizing machinery with different operational cycles.
Methods for Calculating LCM
There are several effective methods to determine the LCM of two or more numbers. We'll explore the most common approaches:
1. Listing Multiples Method
This method is straightforward but can be time-consuming for larger numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, ...
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, ...
By comparing the lists, we observe that the smallest common multiple is 126. Therefore, the LCM(14, 18) = 126. While simple for smaller numbers, this approach becomes less efficient as the numbers increase in size.
2. Prime Factorization Method
This method is generally more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present in the factorizations.
Let's break down 14 and 18 into their prime factors:
- 14 = 2 x 7
- 18 = 2 x 3 x 3 = 2 x 3²
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3² = 9
- Highest power of 7: 7¹ = 7
Now, we multiply these highest powers together:
LCM(14, 18) = 2 x 3² x 7 = 2 x 9 x 7 = 126
This method is significantly more efficient than the listing method, particularly when dealing with larger numbers or a greater number of integers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of two numbers are related through a simple formula:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 14 and 18. We can use the Euclidean algorithm for this:
- Divide the larger number (18) by the smaller number (14): 18 = 14 x 1 + 4
- Replace the larger number with the smaller number (14) and the smaller number with the remainder (4): 14 = 4 x 3 + 2
- Repeat: 4 = 2 x 2 + 0
The last non-zero remainder is the GCD, which is 2.
Now, we can use the formula:
LCM(14, 18) = (14 x 18) / GCD(14, 18) = (14 x 18) / 2 = 252 / 2 = 126
This method provides an alternative approach, especially useful when calculating the LCM of larger numbers where finding the prime factorization might be more challenging.
Real-World Applications of LCM
The concept of LCM extends beyond abstract mathematical exercises. Here are some practical scenarios where understanding LCM proves beneficial:
-
Scheduling Bus Routes: Two bus routes, one running every 14 minutes and the other every 18 minutes, depart from the same station at the same time. The LCM (126 minutes) tells us when both buses will depart simultaneously again. This information is crucial for scheduling and coordinating public transportation.
-
Fraction Addition: To add fractions with different denominators, like 1/14 and 1/18, we need a common denominator. The LCM (126) serves as the least common denominator, making the addition straightforward: (9/126) + (7/126) = 16/126.
-
Music Composition: In music theory, rhythms and melodies often involve repeating patterns. Understanding LCM helps composers synchronize different rhythmic patterns and create harmonious musical structures. For example, two musical phrases with lengths of 14 and 18 beats will align again after 126 beats.
Conclusion: Mastering LCM Calculations
Finding the LCM of 14 and 18, as we've demonstrated, yields a result of 126. This seemingly simple calculation underlines a fundamental concept with widespread practical applications. While the listing method provides a basic understanding, the prime factorization and GCD methods offer more efficient approaches, especially when dealing with larger numbers. Mastering these methods equips you with a valuable mathematical tool applicable in diverse fields, from scheduling and fraction arithmetic to music composition and engineering. The ability to efficiently determine LCMs isn't just about solving mathematical problems; it's about understanding the underlying principles and applying them to real-world situations. This understanding allows for efficient problem-solving and effective coordination in various aspects of life. So, next time you encounter a problem requiring the determination of a least common multiple, remember the methods outlined here, and you'll be well-equipped to find the solution quickly and accurately.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 14 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.