What Is The Lcm Of 2 And 11
News Co
Apr 11, 2025 · 5 min read
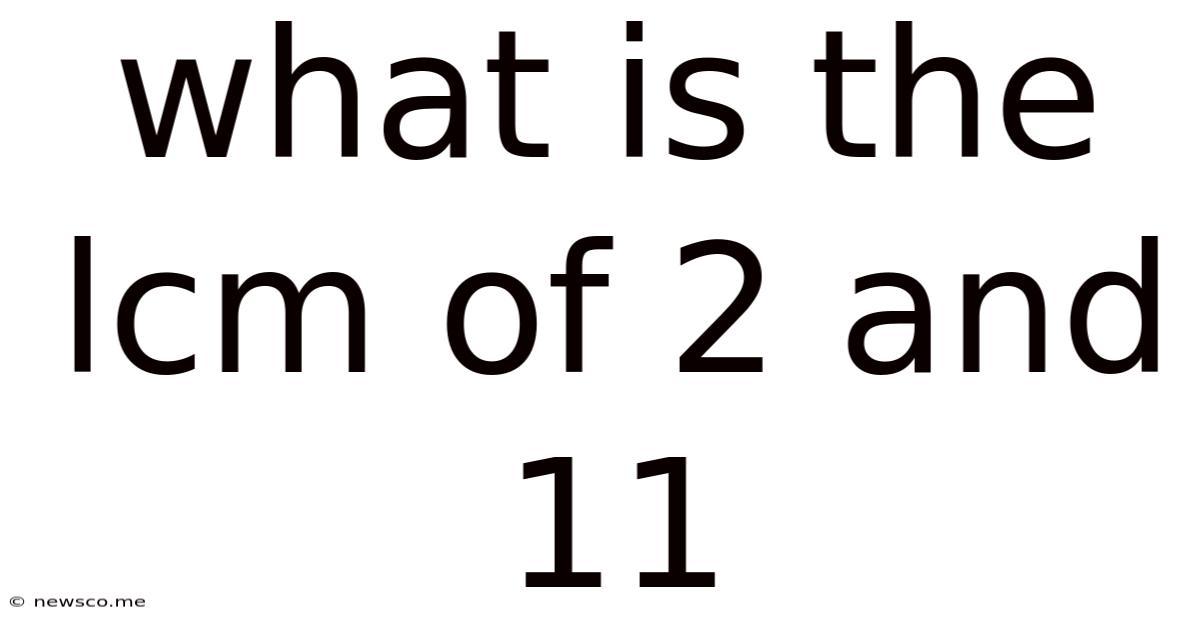
Table of Contents
What is the LCM of 2 and 11? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. It's crucial for simplifying fractions, solving problems involving ratios and proportions, and understanding rhythmic patterns in music. This article will not only answer the question, "What is the LCM of 2 and 11?" but will also provide a comprehensive understanding of LCMs, exploring various methods for calculating them and showcasing their real-world applications.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Key Differences between LCM and GCD: Often, the LCM is discussed alongside the greatest common divisor (GCD). While the LCM is the smallest common multiple, the GCD is the largest common divisor. They are inversely related; understanding one helps grasp the other. For example, the GCD of 12 and 18 is 6, and their LCM is 36. Notice that 6 x 36 = 12 x 18; this relationship holds true for all pairs of integers.
Calculating the LCM of 2 and 11
Now, let's tackle the specific question: What is the LCM of 2 and 11?
Since 2 and 11 are both prime numbers (meaning they are only divisible by 1 and themselves), finding their LCM is straightforward. Prime numbers only have 1 and themselves as factors. Therefore, the only common multiple of 2 and 11 is their product.
The LCM of 2 and 11 is 22.
This is because 22 is the smallest positive integer divisible by both 2 and 11. No smaller number satisfies this condition.
Methods for Calculating LCM
Several methods exist for calculating the LCM of two or more integers. Let's explore the most common approaches:
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24...
- Multiples of 11: 11, 22, 33, 44...
As you can see, the smallest common multiple of 2 and 11 is 22. This method is simple for smaller numbers but becomes cumbersome with larger numbers.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. The LCM is found by taking the highest power of each prime factor present in the factorizations.
- Prime factorization of 2: 2¹
- Prime factorization of 11: 11¹
The prime factors are 2 and 11. Taking the highest power of each, we get 2¹ x 11¹ = 22. Therefore, the LCM is 22. This method is efficient for larger numbers, especially when dealing with multiple numbers.
3. Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This formula connects the LCM and GCD. First, we need to find the GCD of the two numbers. The GCD of 2 and 11 is 1 (since they are coprime – they share no common factors other than 1).
Applying the formula: LCM(2, 11) = (|2 x 11|) / GCD(2, 11) = 22 / 1 = 22
This method is particularly useful when the GCD is easily determined.
Real-World Applications of LCM
The concept of LCM has practical applications in various fields:
1. Scheduling and Timing
Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 2 hours, and another arrives every 11 hours. To find out when both buses will arrive at the bus stop simultaneously, you need to calculate the LCM of 2 and 11, which is 22. Both buses will arrive together after 22 hours.
2. Fraction Operations
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator. This simplifies the process of adding or subtracting fractions.
3. Gear Ratios and Mechanical Systems
In mechanical engineering, gear ratios and other systems often rely on understanding multiples and common multiples. LCM calculations are important in determining synchronization and optimal gear configurations.
4. Music and Rhythm
Musical rhythms and patterns can be analyzed using LCM. For example, understanding when different rhythmic patterns will align requires finding their LCM.
5. Construction and Measurement
Construction projects frequently involve using measurements that are multiples of different units. LCM can be used to simplify calculations and ensure consistent measurements.
Beyond the Basics: LCM of More Than Two Numbers
The principles for calculating the LCM extend to more than two numbers. You can use the prime factorization method or iterative application of the two-number LCM method to solve these problems. For instance, to find the LCM of 2, 3, and 5, you would first find the LCM of 2 and 3 (which is 6), then find the LCM of 6 and 5 (which is 30).
Conclusion: The Importance of Understanding LCM
The ability to find the LCM of numbers is a cornerstone of mathematical proficiency. While the LCM of 2 and 11, which is 22, is a relatively simple calculation, understanding the underlying concepts and methods enables you to tackle more complex problems in various contexts. Mastering LCM calculations is essential for success in many academic and practical situations. From scheduling events to simplifying complex fraction operations, the application of LCM is widespread and significant. This article aimed not just to answer the question but also to equip you with the knowledge and understanding to confidently tackle any LCM calculation you encounter.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 2 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.