What Is The Lcm Of 24 And 30
News Co
Mar 17, 2025 · 5 min read
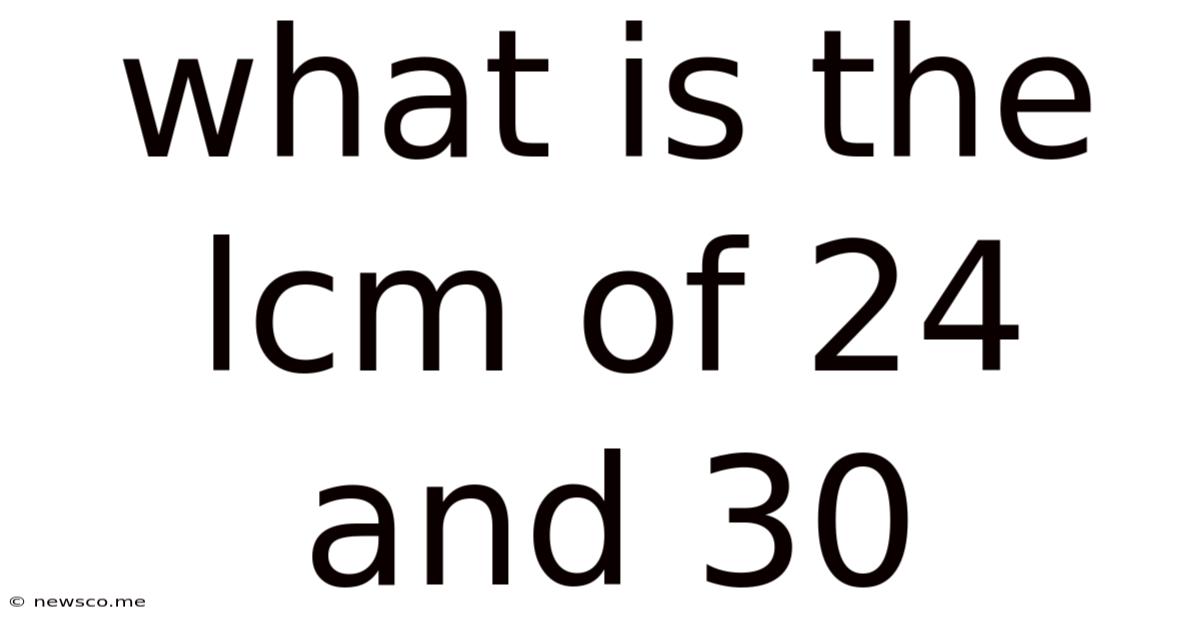
Table of Contents
What is the LCM of 24 and 30? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculation opens doors to more advanced mathematical concepts. This article will delve into the question, "What is the LCM of 24 and 30?", exploring different approaches to finding the answer and highlighting the broader significance of LCMs in mathematics and real-world applications.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 24 and 30, let's establish a solid understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, ... and multiples of 3 are 3, 6, 9, 12, 15, ... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
One straightforward method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to 24 and 30:
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240...
- Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240...
As we can see, the smallest number that appears in both lists is 120. Therefore, the LCM of 24 and 30 is 120. This method is simple for smaller numbers, but it becomes less efficient as the numbers increase in size.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves using prime factorization. This method relies on breaking down each number into its prime factors – the prime numbers that multiply together to give the original number.
Let's find the prime factorization of 24 and 30:
- 24 = 2³ x 3¹ (24 is 2 x 2 x 2 x 3)
- 30 = 2¹ x 3¹ x 5¹ (30 is 2 x 3 x 5)
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(24, 30) = 2³ x 3¹ x 5¹ = 8 x 3 x 5 = 120
This method is generally more efficient and less prone to errors than simply listing multiples, especially when dealing with larger numbers or multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both integers without leaving a remainder. There's a handy formula that connects the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 24 and 30 using the Euclidean algorithm:
- Divide the larger number (30) by the smaller number (24): 30 ÷ 24 = 1 with a remainder of 6.
- Replace the larger number with the smaller number (24) and the smaller number with the remainder (6): 24 ÷ 6 = 4 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 6. Therefore, GCD(24, 30) = 6.
Now, we can use the formula:
LCM(24, 30) = (24 x 30) / GCD(24, 30) = (720) / 6 = 120
This method provides an alternative approach and demonstrates the relationship between LCM and GCD.
Real-World Applications of LCM
Understanding LCMs is not just an abstract mathematical exercise; it has practical applications in various fields:
-
Scheduling: Imagine two buses depart from the same station, one every 24 minutes and the other every 30 minutes. To find out when they will depart together again, you need to find the LCM of 24 and 30, which is 120 minutes (or 2 hours).
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator.
-
Project Management: In project planning, if different tasks have different cycle times, finding the LCM can help determine when all tasks will be completed simultaneously.
-
Music: In music theory, LCM is used to determine the least common multiple of note durations, which affects the rhythmic structure of a piece.
-
Gear Ratios: In mechanical engineering, LCM is used in calculating gear ratios to synchronize the rotational speeds of different gears.
Conclusion: The Significance of LCM(24, 30) = 120
Through different methods, we have conclusively determined that the least common multiple of 24 and 30 is 120. This seemingly simple calculation highlights the broader importance of understanding LCMs in various mathematical contexts and its practical applications in diverse fields. By mastering different techniques for finding the LCM, one can efficiently solve problems and gain a deeper appreciation for the interconnectedness of mathematical concepts. Remember to choose the method that best suits the numbers involved – listing multiples for smaller numbers and prime factorization or the GCD method for larger numbers. The understanding of LCM is a fundamental building block for many more complex mathematical concepts, making it a valuable skill to develop. The simple problem of finding LCM(24, 30) serves as a gateway to understanding a powerful mathematical tool with far-reaching applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 24 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.