What Is The Lcm Of 25 And 20
News Co
Mar 22, 2025 · 4 min read
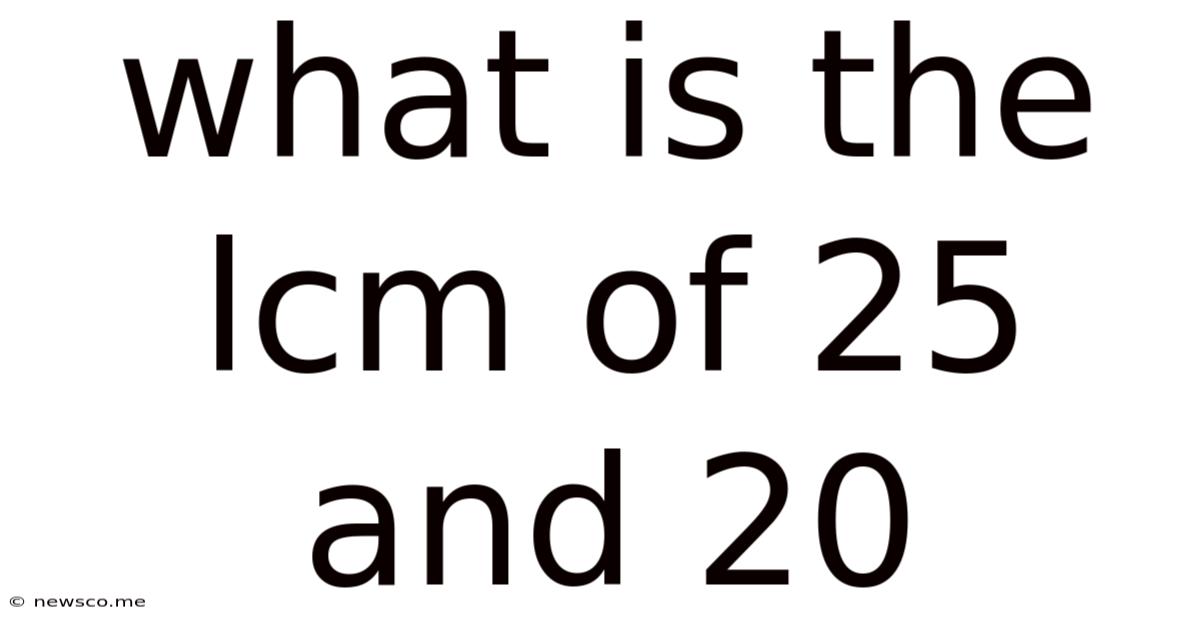
Table of Contents
What is the LCM of 25 and 20? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple mathematical task, but understanding the underlying concepts and different methods for calculating it can be surprisingly insightful. This comprehensive guide will explore the LCM of 25 and 20, delving into the various approaches and showcasing their practical applications. We’ll move beyond the simple answer and explore the broader significance of LCM in mathematics and real-world scenarios.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 25 and 20, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that both of your original numbers can divide into evenly.
Key characteristics of LCM:
- Positive Integer: The LCM is always a positive whole number.
- Smallest Multiple: It represents the smallest number divisible by all the given numbers.
- Application in Various Fields: LCM finds applications in various fields, including scheduling, music theory, and even computer science.
Methods for Calculating LCM
There are several ways to calculate the LCM, each with its own advantages and disadvantages. Let’s explore the most common approaches:
1. Listing Multiples Method
This is a straightforward method, especially for smaller numbers. We simply list the multiples of each number until we find the smallest common multiple.
Multiples of 25: 25, 50, 75, 100, 125, 150, 175, 200...
Multiples of 20: 20, 40, 60, 80, 100, 120, 140, 160, 180, 200...
By comparing the lists, we can see that the smallest common multiple of 25 and 20 is 100.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors.
- Prime Factorization of 25: 5 x 5 = 5²
- Prime Factorization of 20: 2 x 2 x 5 = 2² x 5
To find the LCM, we take the highest power of each prime factor present in the factorizations and multiply them together:
LCM(25, 20) = 2² x 5² = 4 x 25 = 100
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers evenly. The relationship is expressed as:
LCM(a, b) x GCD(a, b) = a x b
First, we find the GCD of 25 and 20 using the Euclidean algorithm or prime factorization:
- Prime Factorization of 25: 5²
- Prime Factorization of 20: 2² x 5
The common prime factor is 5 (to the power of 1). Therefore, GCD(25, 20) = 5.
Now, we can use the formula:
LCM(25, 20) = (25 x 20) / GCD(25, 20) = 500 / 5 = 100
Choosing the Right Method
The best method for calculating the LCM depends on the numbers involved.
- Listing Multiples: Suitable for small numbers where the multiples are easily identifiable.
- Prime Factorization: Efficient for larger numbers and provides a deeper understanding of the mathematical principles involved.
- GCD Method: Efficient for larger numbers, particularly when the GCD is easily determined.
Real-World Applications of LCM
The concept of LCM extends far beyond the classroom. Here are some examples:
-
Scheduling: Imagine two buses depart from the same station, one every 25 minutes and the other every 20 minutes. The LCM (100 minutes) tells us when both buses will depart simultaneously again.
-
Music Theory: LCM helps determine the least common denominator when working with musical rhythms and time signatures.
-
Construction and Engineering: LCM plays a crucial role in tasks like aligning beams or arranging tiles based on specific dimensions, which have to be divisible by whole units.
-
Computer Science: In tasks like memory allocation and process synchronization, the LCM concept helps optimize resource usage and avoid conflicts.
Beyond the Basics: Exploring LCM with More Numbers
While we've focused on the LCM of two numbers, the concept extends easily to three or more numbers. The methods discussed above, particularly prime factorization, can be adapted to handle multiple numbers.
For instance, let's find the LCM of 25, 20, and 15:
- Prime Factorization of 25: 5²
- Prime Factorization of 20: 2² x 5
- Prime Factorization of 15: 3 x 5
The LCM would be 2² x 3 x 5² = 4 x 3 x 25 = 300
Conclusion: Mastering LCM for Enhanced Mathematical Understanding
Understanding the LCM is crucial for various mathematical applications and real-world problem-solving. Whether using the listing method for small numbers or the prime factorization method for larger ones, the ability to efficiently calculate the LCM demonstrates a strong grasp of fundamental mathematical principles. This knowledge extends beyond simple calculations and enables one to solve complex scheduling, timing, and synchronization issues across many fields. The exploration of different methods and their underlying principles provides a richer and more versatile understanding of this essential concept. Remember, practice is key to mastering this vital mathematical skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 25 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.