What Is The Lcm Of 3 5 And 6
News Co
Apr 17, 2025 · 5 min read
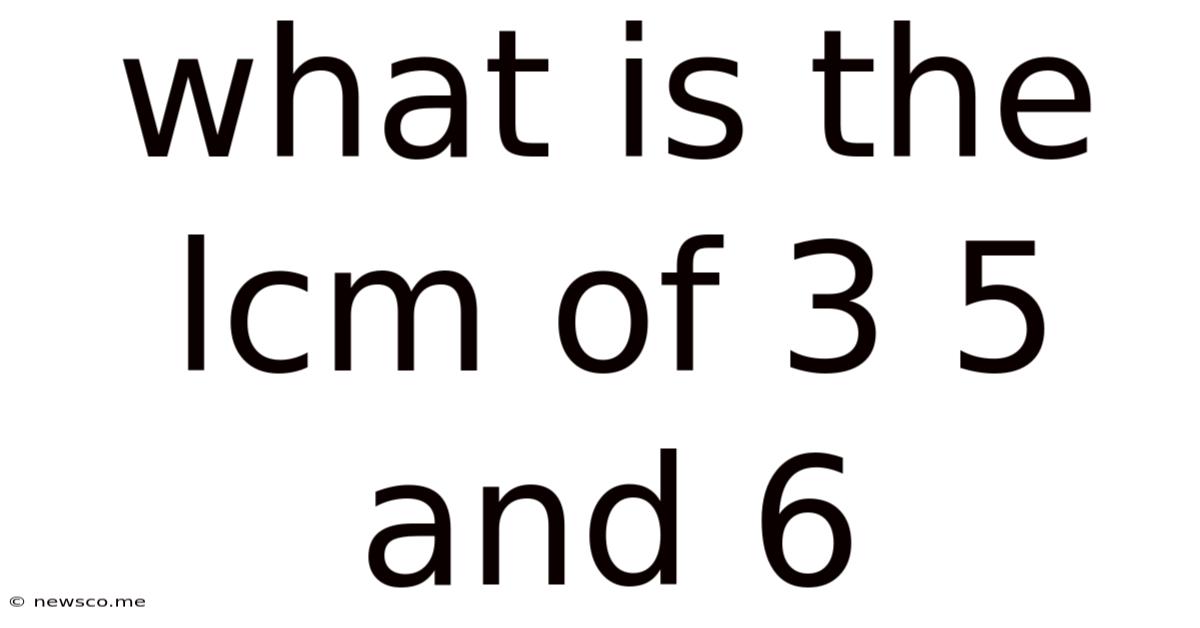
Table of Contents
What is the LCM of 3, 5, and 6? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex problems in algebra and number theory. This article will comprehensively explore how to calculate the LCM of 3, 5, and 6, explaining the different methods available and providing a deeper understanding of the underlying principles. We'll also touch upon the practical applications of LCMs and offer some helpful tips for mastering this essential mathematical skill.
Understanding Least Common Multiples (LCM)
Before diving into the calculation, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple, therefore, is 6.
Methods for Calculating the LCM of 3, 5, and 6
There are several ways to find the LCM of 3, 5, and 6. We will explore two primary methods: the listing method and the prime factorization method. Both methods are effective, but the prime factorization method is generally more efficient, especially when dealing with larger numbers.
Method 1: The Listing Method
This method involves listing the multiples of each number until a common multiple is found. While straightforward for smaller numbers, it becomes cumbersome and inefficient for larger sets or larger numbers.
Let's apply this to our numbers, 3, 5, and 6:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 6: 6, 12, 18, 24, 30...
By comparing the lists, we can see that the smallest common multiple of 3, 5, and 6 is 30. Therefore, the LCM(3, 5, 6) = 30.
Method 2: The Prime Factorization Method
This method is generally preferred for its efficiency, especially with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Let's break down each number into its prime factors:
- 3: 3 (3 is a prime number)
- 5: 5 (5 is a prime number)
- 6: 2 x 3
Now, we identify the unique prime factors present in all three numbers: 2, 3, and 5. We take the highest power of each prime factor:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Finally, we multiply these highest powers together: 2 x 3 x 5 = 30. Therefore, the LCM(3, 5, 6) = 30 using the prime factorization method.
Why is the LCM Important?
Understanding and calculating LCMs is crucial for various mathematical operations and real-world applications. Here are a few key examples:
1. Adding and Subtracting Fractions
Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators. For instance, to add 1/3 + 1/5 + 1/6, we need the LCM of 3, 5, and 6, which is 30. We then rewrite each fraction with a denominator of 30 before performing the addition.
2. Solving Problems Involving Cycles or Periodic Events
LCMs are essential for solving problems involving cyclical events that repeat at different intervals. Consider scenarios like:
- Meeting Scheduling: Two friends want to meet regularly. One is available every 3 days, the other every 5 days. The LCM(3, 5) = 15 indicates they can meet every 15 days.
- Gear Ratios: In mechanics, gear ratios are often expressed using LCMs to determine the least common rotational period of interacting gears.
- Calendars and Time: Finding the next time multiple events coincide (e.g., when a specific day of the week falls on a specific date) utilizes LCM calculations.
3. Number Theory and Abstract Algebra
LCMs play a significant role in advanced mathematical fields such as number theory and abstract algebra, where they are used to solve complex equations and explore the properties of integers.
Tips for Mastering LCM Calculations
- Practice Regularly: The more you practice, the more comfortable and efficient you'll become in calculating LCMs.
- Start with the Basics: Master the listing method for smaller numbers before moving on to the prime factorization method.
- Understand Prime Factorization: A strong grasp of prime factorization is essential for efficiently using the prime factorization method.
- Use Online Calculators (for verification): While it's important to understand the underlying principles, online calculators can be used to verify your calculations, especially when dealing with larger numbers. However, always ensure you understand the process first.
- Relate it to real-world problems: Try applying LCM concepts to real-world scenarios to improve your understanding and retention.
Conclusion
Calculating the least common multiple is a fundamental mathematical skill with broad applications. Whether you employ the listing method or the more efficient prime factorization method, understanding the concept and its practical implications is vital for success in various mathematical and real-world contexts. The LCM of 3, 5, and 6 is definitively 30, a result obtained through both methods, highlighting the consistency and reliability of these approaches. By mastering LCM calculations, you equip yourself with a powerful tool for tackling a wide array of mathematical problems and gaining a deeper appreciation of numerical relationships. Continuous practice and a focus on understanding the underlying principles will solidify your mastery of this essential concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.