What Is The Lcm Of 3 And 9
News Co
Mar 15, 2025 · 5 min read
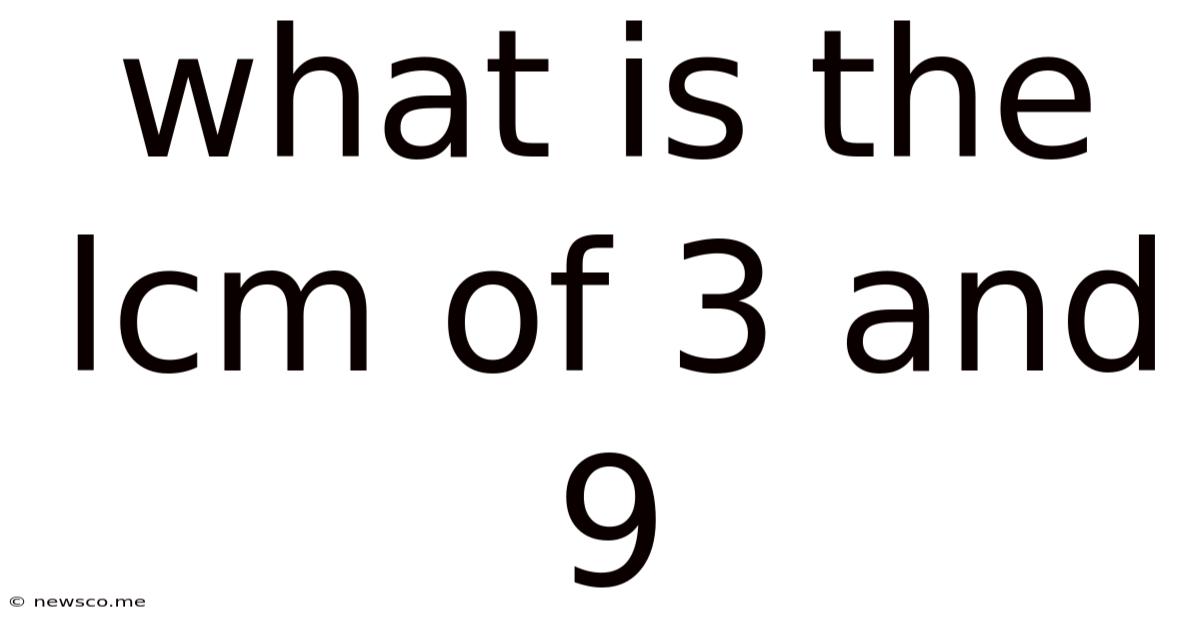
Table of Contents
What is the LCM of 3 and 9? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and even advanced topics like number theory. This article will explore the LCM of 3 and 9 in detail, providing a comprehensive understanding of the concept and various methods to calculate it. We'll move beyond a simple answer, delving into the underlying principles and demonstrating how this seemingly basic calculation forms a cornerstone of more complex mathematical operations.
Understanding Least Common Multiples (LCM)
Before we tackle the specific LCM of 3 and 9, let's solidify our understanding of what an LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the numbers as factors.
For example, consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20, and so on. The multiples of 6 are 6, 12, 18, 24, and so on. The common multiples of 4 and 6 are 12, 24, 36, and so forth. The least common multiple, therefore, is 12.
Method 1: Listing Multiples
The most straightforward method to find the LCM, especially for smaller numbers like 3 and 9, is by listing their multiples.
Step 1: List the multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24...
Step 2: List the multiples of 9: 9, 18, 27, 36, 45...
Step 3: Identify the common multiples: 9, 18, 27...
Step 4: Determine the least common multiple: The smallest common multiple is 9.
Therefore, the LCM of 3 and 9 is 9.
Method 2: Prime Factorization
Prime factorization is a more powerful method that works efficiently for larger numbers and provides a deeper understanding of the underlying mathematical structure. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 3
3 is a prime number, so its prime factorization is simply 3.
Step 2: Prime Factorization of 9
9 can be factored as 3 x 3, or 3².
Step 3: Identifying Common and Unique Factors
Comparing the prime factorizations, we see that both 3 and 9 share the prime factor 3. However, 9 has an additional factor of 3.
Step 4: Calculating the LCM
To find the LCM, we take the highest power of each prime factor present in either factorization. In this case, the highest power of 3 is 3² (or 9).
Therefore, the LCM of 3 and 9 is 9.
Method 3: Using the Formula (for Two Numbers)
For two numbers, a and b, there's a convenient formula relating the LCM and the greatest common divisor (GCD):
LCM(a, b) = (|a * b|) / GCD(a, b)
Where |a * b| represents the absolute value of the product of a and b.
Step 1: Finding the GCD of 3 and 9
The greatest common divisor is the largest number that divides both 3 and 9 without leaving a remainder. In this case, the GCD of 3 and 9 is 3.
Step 2: Applying the Formula
LCM(3, 9) = (|3 * 9|) / GCD(3, 9) = 27 / 3 = 9
Therefore, the LCM of 3 and 9 is 9.
Why is the LCM Important?
The LCM isn't just an abstract mathematical concept; it has practical applications across various mathematical fields and real-world scenarios.
-
Adding and Subtracting Fractions: To add or subtract fractions with different denominators, you need to find a common denominator, which is typically the LCM of the denominators. This ensures accurate and simplified results. For example, adding 1/3 and 1/9 requires finding the LCM of 3 and 9 (which is 9), allowing us to rewrite the fractions as 3/9 and 1/9 before adding them.
-
Solving Problems Involving Cycles or Periods: LCM is crucial in problems involving cyclical events. For example, if two events occur at intervals of 3 and 9 days, respectively, the LCM helps determine when both events will occur simultaneously again. In this case, the LCM of 3 and 9 (which is 9) indicates that both events will coincide every 9 days.
-
Scheduling and Planning: In project management or scheduling tasks, LCM can help synchronize activities that have different durations or repetition patterns. Finding the LCM ensures efficient coordination of resources and minimizes delays.
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly useful for this. Let's find the LCM of 3, 6, and 9:
Step 1: Prime Factorization
- 3 = 3
- 6 = 2 x 3
- 9 = 3²
Step 2: Identifying Highest Powers
The highest power of 2 is 2¹ The highest power of 3 is 3²
Step 3: Calculating the LCM
LCM(3, 6, 9) = 2¹ x 3² = 2 x 9 = 18
Conclusion: The Significance of a Simple Calculation
While the LCM of 3 and 9 might seem like a trivial calculation, it serves as a foundation for a broader understanding of number theory and its practical applications. Mastering the various methods for calculating LCMs, from simple listing to sophisticated prime factorization, equips you with a valuable tool for problem-solving across multiple mathematical disciplines and real-world situations. Understanding the LCM is not simply about finding the answer; it’s about grasping the fundamental principles that underpin a significant portion of mathematical operations. This detailed exploration aims to provide more than just the answer – it provides a robust understanding of the concept and its far-reaching importance.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.