What Is The Lcm Of 36 And 54
News Co
Mar 22, 2025 · 5 min read
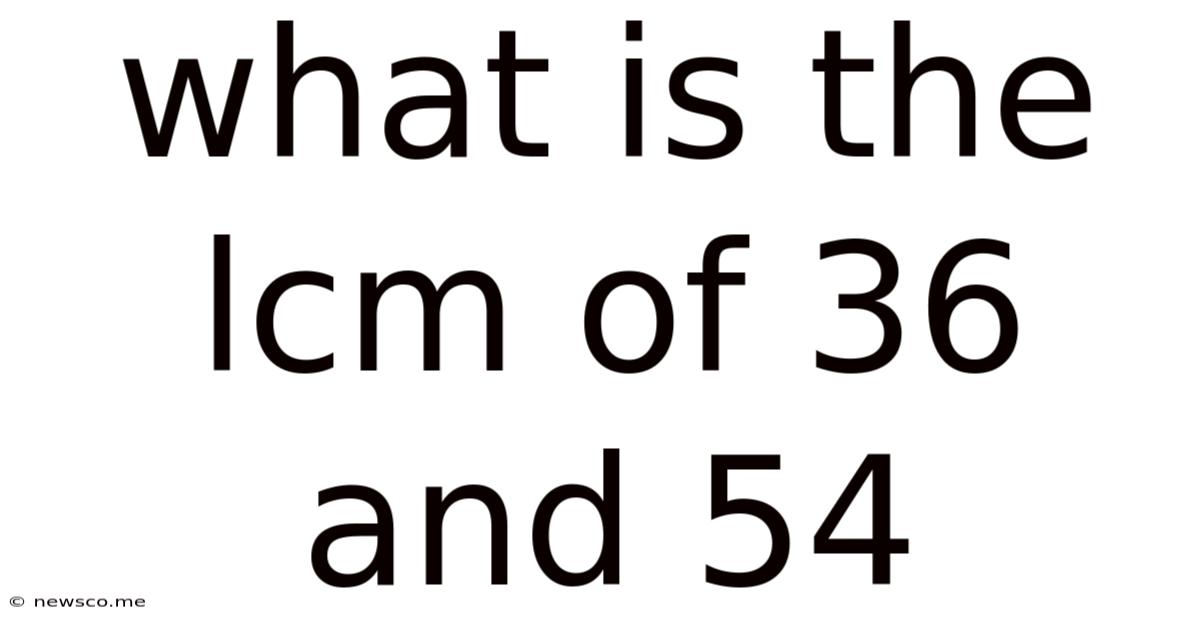
Table of Contents
What is the LCM of 36 and 54? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it can be surprisingly insightful. This comprehensive guide will not only answer the question "What is the LCM of 36 and 54?" but will also explore the broader topic of LCMs, offering various approaches and practical applications.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors. This concept is fundamental in various areas of mathematics, including fraction simplification, solving problems related to cycles (like in scheduling), and understanding rhythmic patterns in music.
For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24…
The common multiples of 2 and 3 are 6, 12, 18, 24, and so on. The least common multiple is 6.
Methods for Finding the LCM
Several methods exist for calculating the LCM of two or more numbers. We'll explore the most common and efficient approaches:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. Simply list the multiples of each number until you find the smallest multiple that is common to both. While effective for small numbers, it becomes inefficient for larger ones.
Let's use this method for 36 and 54:
- Multiples of 36: 36, 72, 108, 144, 180, 216, 252, 288, 324, 360...
- Multiples of 54: 54, 108, 162, 216, 270, 324, 378...
Notice that 108 appears in both lists. However, a smaller common multiple, 108, appears earlier. Therefore, the LCM of 36 and 54 is 108.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Prime Factorization of 36:
36 = 2 x 2 x 3 x 3 = 2² x 3²
Prime Factorization of 54:
54 = 2 x 3 x 3 x 3 = 2 x 3³
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2² = 4
- Highest power of 3: 3³ = 27
LCM(36, 54) = 2² x 3³ = 4 x 27 = 108
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) = (a x b) / GCD(a, b)
First, we need to find the GCD of 36 and 54. We can use the Euclidean algorithm for this:
- Divide the larger number (54) by the smaller number (36): 54 ÷ 36 = 1 with a remainder of 18.
- Replace the larger number with the smaller number (36) and the smaller number with the remainder (18): 36 ÷ 18 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 18.
Now, we can calculate the LCM:
LCM(36, 54) = (36 x 54) / 18 = 1944 / 18 = 108
Why is understanding LCM important?
The concept of LCM extends beyond simple mathematical exercises. It has several practical applications:
1. Fraction Addition and Subtraction:
Finding the LCM of the denominators is crucial when adding or subtracting fractions. This ensures that you are working with equivalent fractions that have a common denominator, enabling easy addition or subtraction.
For example, to add 1/36 + 1/54, the LCM of 36 and 54 (which is 108) is needed to find the common denominator.
2. Scheduling and Cyclical Events:
LCM is essential in solving problems related to recurring events that happen at different intervals. For example, imagine two buses that depart from a station at different intervals. The LCM of their departure intervals helps determine when both buses will depart at the same time.
3. Music and Rhythm:
In music theory, the LCM helps determine when different rhythmic patterns will coincide. Understanding LCM is useful for composing music and analyzing musical structures.
4. Gear Ratios and Mechanical Systems:
In mechanical engineering, LCM plays a role in calculating gear ratios and optimizing the efficiency of mechanical systems.
5. Computer Science and Algorithms:
LCM is used in various algorithms and data structures in computer science, particularly in areas like scheduling and resource allocation.
Beyond the Basics: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply include all prime factors from the factorizations of all the numbers, taking the highest power of each. For the GCD method, you can find the LCM iteratively, calculating the LCM of two numbers at a time and then finding the LCM of the result with the next number, and so on.
Conclusion: The Power of the LCM
The seemingly simple concept of the least common multiple holds significant importance across various fields. Mastering different methods for calculating the LCM, such as prime factorization and the GCD method, equips you with powerful tools for solving a wide range of problems, far exceeding the basic arithmetic applications. Understanding the LCM provides a deeper appreciation for the interconnectedness of mathematical concepts and their practical implications in diverse domains. In this detailed exploration, we conclusively determined that the LCM of 36 and 54 is indeed 108. Hopefully, this comprehensive guide has not only answered your initial question but also broadened your understanding and appreciation of this crucial mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 36 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.