What Is The Lcm Of 4 6 9
News Co
Mar 22, 2025 · 5 min read
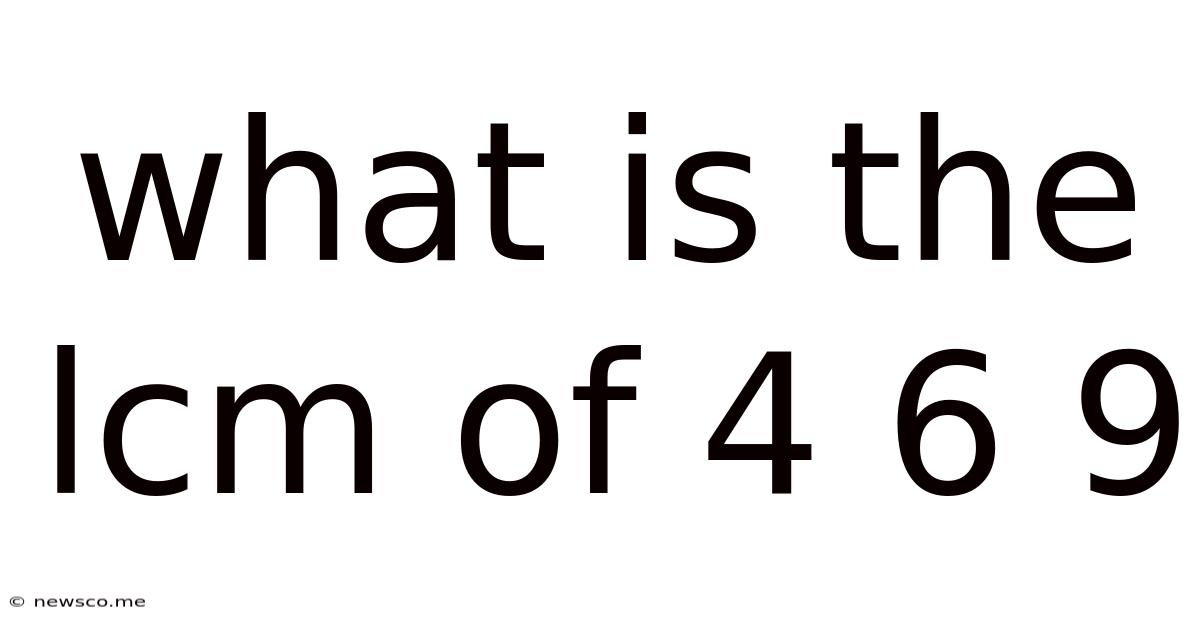
Table of Contents
What is the LCM of 4, 6, and 9? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with wide-ranging applications in various fields, from scheduling tasks to simplifying fractions. This article will explore the LCM of 4, 6, and 9 in detail, providing a comprehensive understanding of the process and its underlying principles. We'll delve into multiple methods for calculating the LCM, discussing their advantages and disadvantages, and ultimately demonstrate how to solve this specific problem and similar ones effectively.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. It's essentially the smallest number that contains all the given numbers as factors. Understanding LCM is crucial for simplifying fractions, solving problems related to cycles and periodic events, and various other mathematical operations.
Why is LCM important?
The applications of LCM extend far beyond the realm of pure mathematics:
- Scheduling: Imagine you have three tasks that repeat on different cycles – one every 4 days, another every 6 days, and a third every 9 days. The LCM will tell you when all three tasks coincide, allowing for efficient scheduling.
- Fraction Simplification: Finding the LCM of the denominators is essential when adding or subtracting fractions with different denominators. It allows you to find a common denominator for easier calculation.
- Modular Arithmetic: LCM plays a crucial role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
- Music Theory: Understanding LCM helps in understanding musical intervals and harmonies.
Methods for Finding the LCM of 4, 6, and 9
Several methods exist for calculating the LCM of a set of numbers. We'll explore three common approaches:
1. Listing Multiples Method
This method involves listing the multiples of each number until you find the smallest multiple common to all.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42...
- Multiples of 9: 9, 18, 27, 36, 45...
By comparing the lists, we can see that the smallest multiple common to all three numbers is 36. This method is straightforward for small numbers but becomes cumbersome and inefficient for larger numbers.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the highest powers of all prime factors present.
- Prime factorization of 4: 2²
- Prime factorization of 6: 2 × 3
- Prime factorization of 9: 3²
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2² = 4
- Highest power of 3: 3² = 9
Multiply these highest powers together: 4 × 9 = 36. Therefore, the LCM of 4, 6, and 9 is 36.
This method is generally more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of a set of numbers are related through the following formula:
LCM(a, b) × GCD(a, b) = a × b
This relationship holds for two numbers. To extend this to three or more numbers, we can use a stepwise approach:
-
Find the GCD of two numbers: Let's find the GCD of 4 and 6 using the Euclidean algorithm:
- 6 = 1 × 4 + 2
- 4 = 2 × 2 + 0 The GCD(4, 6) is 2.
-
Find the LCM of the two numbers: Using the formula: LCM(4, 6) = (4 × 6) / GCD(4, 6) = 24 / 2 = 12
-
Repeat for the next number: Now, find the GCD of 12 and 9:
- 12 = 1 × 9 + 3
- 9 = 3 × 3 + 0 The GCD(12, 9) is 3.
-
Find the LCM: LCM(12, 9) = (12 × 9) / GCD(12, 9) = 108 / 3 = 36
This method is useful when you already know the GCD of some of the numbers.
Why 36 is the LCM of 4, 6, and 9: A Detailed Explanation
The LCM of 4, 6, and 9 is 36 because 36 is the smallest positive integer that is divisible by 4, 6, and 9 without leaving a remainder. Let's verify this:
- 36 ÷ 4 = 9
- 36 ÷ 6 = 6
- 36 ÷ 9 = 4
No smaller positive integer satisfies this condition. Any other common multiple of 4, 6, and 9 (like 72, 108, etc.) will be a multiple of 36. Therefore, 36 is the least common multiple.
Applications of LCM in Real-World Scenarios
The concept of LCM isn't confined to abstract mathematical exercises; it finds practical application in numerous real-world situations:
- Construction: Determining the appropriate lengths of materials for tiling or flooring projects often involves finding the LCM to ensure seamless alignment.
- Manufacturing: In assembly line processes, determining the optimal production cycle might necessitate using LCM to synchronize different stages of manufacturing.
- Music: LCM is crucial in music theory for understanding rhythmic patterns and the harmonization of different musical phrases. It helps determine when different musical lines will coincide.
- Calendars: Calculating when events that recur at different intervals will occur on the same day often relies on finding the LCM.
Conclusion: Mastering LCM Calculations
Finding the least common multiple is a fundamental skill in mathematics with wide-ranging applications. We've explored various methods for determining the LCM, including listing multiples, prime factorization, and the GCD method. The prime factorization method is generally the most efficient, especially for larger numbers. Understanding LCM is not only crucial for academic success but also for solving real-world problems across various disciplines, from scheduling tasks to simplifying complex calculations. By mastering these techniques, you'll enhance your mathematical skills and equip yourself with a valuable tool for solving numerous problems efficiently. Remember that practicing different methods will help you solidify your understanding and choose the most appropriate approach for each specific scenario. The specific example of finding the LCM of 4, 6, and 9 serves as an excellent starting point for mastering this essential mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 4 6 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.