What Is The Lcm Of 6 8 12
News Co
Mar 21, 2025 · 5 min read
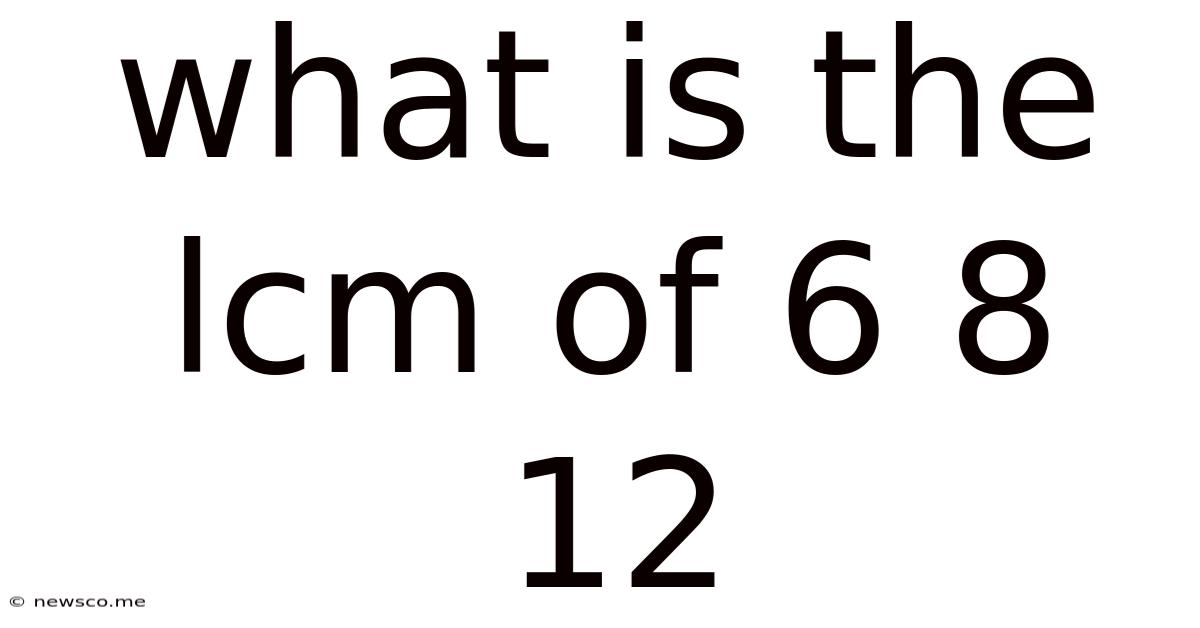
Table of Contents
What is the LCM of 6, 8, and 12? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications spanning various fields, from scheduling tasks to simplifying fractions. This comprehensive guide will not only answer the question, "What is the LCM of 6, 8, and 12?" but also provide a thorough understanding of the LCM concept, its calculation methods, and its practical uses.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
This concept is crucial in various mathematical operations, including:
- Simplifying Fractions: Finding the LCM of the denominators allows for the easy addition and subtraction of fractions.
- Solving Equations: The LCM is useful in solving equations involving fractions or multiples.
- Scheduling Problems: Determining the LCM helps in solving problems involving cyclical events that need to be synchronized, such as determining when two machines operating at different cycles will next perform a task simultaneously.
Methods for Calculating the LCM
Several methods can be employed to calculate the LCM of a set of numbers. Let's explore the most common ones:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. List the multiples of each number until you find the smallest multiple common to all.
Let's illustrate with the numbers 6, 8, and 12:
- Multiples of 6: 6, 12, 18, 24, 30, 36, 48, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, ...
- Multiples of 12: 12, 24, 36, 48, ...
The smallest multiple common to all three lists is 24. Therefore, the LCM of 6, 8, and 12 is 24.
This method is simple for smaller numbers but becomes inefficient for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers and involves expressing each number as a product of its prime factors. The LCM is then constructed using the highest power of each prime factor present in the factorizations.
Let's apply this to 6, 8, and 12:
- Prime factorization of 6: 2 x 3
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
To find the LCM, take the highest power of each prime factor present:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
LCM = 2³ x 3 = 8 x 3 = 24
This method is more efficient and systematic, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship can be extended to more than two numbers, although the calculation becomes more complex.
While this method is mathematically elegant, it's often less practical for hand calculations, especially with more than two numbers. It's more suitable for algorithmic implementations.
Answering the Question: LCM of 6, 8, and 12
Using any of the methods described above, we find that the LCM of 6, 8, and 12 is 24. The prime factorization method is arguably the most efficient for this example, clearly showing how the highest powers of the prime factors (2³ and 3¹) combine to give the LCM.
Applications of LCM in Real-World Scenarios
The LCM's applications extend far beyond simple mathematical exercises. Consider these examples:
-
Scheduling Production Lines: Imagine three machines in a factory that produce parts at different rates. Machine A produces a part every 6 minutes, Machine B every 8 minutes, and Machine C every 12 minutes. To synchronize production, we need to find the LCM (24 minutes). Every 24 minutes, all three machines will complete a cycle simultaneously.
-
Recipe Scaling: A recipe calls for ingredients in ratios that are not whole numbers. Finding the LCM of the denominators allows you to scale the recipe up to use whole numbers of ingredients, simplifying the cooking process.
-
Music Synchronization: In music, the LCM is used to find the shortest time interval when multiple musical phrases with different rhythms will end at the same time, creating a pleasing and synchronized musical texture.
-
Project Management: When coordinating tasks with different durations, the LCM can help identify when all tasks will be completed, facilitating better project scheduling and resource allocation.
Beyond the Basics: Exploring LCM with More Numbers
The methods described earlier can be extended to find the LCM of more than three numbers. The prime factorization method remains particularly effective for larger sets of numbers. Simply find the prime factorization of each number, and then multiply together the highest power of each prime factor found across all factorizations.
For example, finding the LCM of 6, 8, 12, and 15:
- 6 = 2 x 3
- 8 = 2³
- 12 = 2² x 3
- 15 = 3 x 5
The highest powers are 2³ (from 8), 3¹ (from 6, 12, and 15), and 5¹ (from 15). Therefore, the LCM is 2³ x 3 x 5 = 120.
Conclusion: Mastering LCM for Mathematical Proficiency
Understanding and calculating the least common multiple is a fundamental skill with far-reaching applications. Whether you're simplifying fractions, scheduling projects, or solving more complex mathematical problems, mastering the LCM will significantly enhance your mathematical proficiency and problem-solving capabilities. This article has explored various methods for calculating the LCM, emphasizing the prime factorization method as the most efficient and versatile approach, particularly when dealing with larger numbers or more complex scenarios. By understanding these concepts and techniques, you'll be well-equipped to tackle a wide range of mathematical challenges confidently and efficiently. Remember, practice is key to mastering this important mathematical concept.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 6 8 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.