What Is The Lcm Of 6 And 11
News Co
Mar 25, 2025 · 5 min read
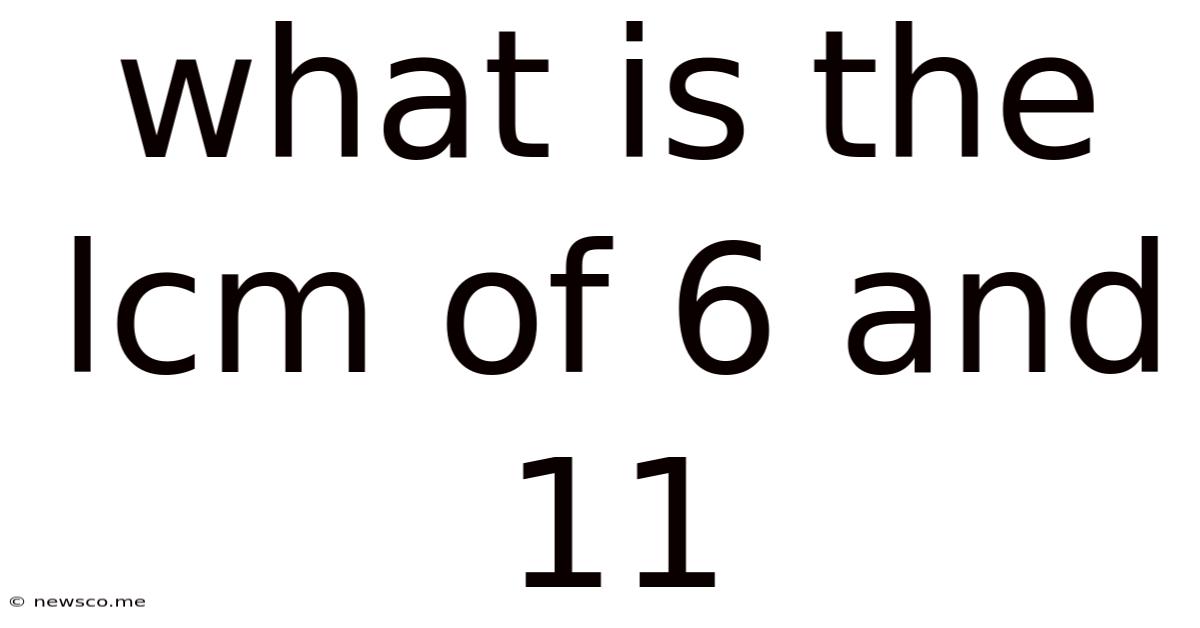
Table of Contents
What is the LCM of 6 and 11? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and algebra. Understanding LCMs is crucial for solving various problems involving fractions, ratios, and rhythmic patterns. This comprehensive guide will not only answer the question, "What is the LCM of 6 and 11?" but also explore the broader concept of LCMs, providing you with the tools and knowledge to calculate them efficiently for any pair of numbers.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer that is divisible by both 2 and 3.
Let's break down the key concepts:
- Multiple: A multiple of a number is the product of that number and any integer. For instance, multiples of 6 are 6, 12, 18, 24, and so on.
- Common Multiple: A common multiple of two or more numbers is a multiple that is shared by all of them. For example, common multiples of 6 and 9 are 18, 36, 54, etc.
- Least Common Multiple (LCM): The smallest of these common multiples is the LCM.
Methods for Calculating LCM
There are several methods to calculate the LCM of two or more numbers. We'll explore the most common and efficient ones:
1. Listing Multiples Method
This method is straightforward but can be time-consuming for larger numbers. It involves listing the multiples of each number until you find the smallest common multiple.
Example: Finding the LCM of 6 and 11
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, ...
- Multiples of 11: 11, 22, 33, 44, 55, 66, ...
The smallest multiple that appears in both lists is 66. Therefore, the LCM of 6 and 11 is 66.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then building the LCM using the highest powers of each prime factor.
Example: Finding the LCM of 6 and 11
-
Prime Factorization:
- 6 = 2 x 3
- 11 = 11 (11 is a prime number)
-
Building the LCM:
- Identify the unique prime factors: 2, 3, and 11.
- Take the highest power of each prime factor: 2¹, 3¹, and 11¹.
- Multiply these highest powers together: 2 x 3 x 11 = 66
Therefore, the LCM of 6 and 11 is 66.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of two numbers are related by the following formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
To use this method, you first need to find the GCD of the two numbers. The Euclidean algorithm is a highly efficient method for finding the GCD.
Example: Finding the LCM of 6 and 11 using the GCD method
-
Finding the GCD of 6 and 11: The GCD of 6 and 11 is 1 (they share only the common divisor 1).
-
Applying the formula: LCM(6, 11) x GCD(6, 11) = 6 x 11 LCM(6, 11) x 1 = 66 LCM(6, 11) = 66
Therefore, the LCM of 6 and 11 is 66.
The LCM of 6 and 11: A Detailed Explanation
As demonstrated using all three methods, the least common multiple of 6 and 11 is 66. This is because 66 is the smallest positive integer that is divisible by both 6 and 11 without leaving a remainder.
Applications of LCM
The concept of LCM has numerous applications across various fields:
- Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It helps in finding a common denominator to simplify the calculations.
- Scheduling: LCM is used to determine when events will occur simultaneously. For example, if two buses leave a station at different intervals, the LCM helps find when they will depart together again.
- Rhythms and Music: In music, LCM helps determine the shortest time it takes for rhythmic patterns to repeat simultaneously.
- Gears and Machines: LCM is used in designing gears and other machine components to synchronize their rotations efficiently.
- Modular Arithmetic: LCM plays a significant role in modular arithmetic, a branch of number theory that deals with remainders after division.
Advanced Concepts and Extensions
The concept of LCM can be extended to more than two numbers. The methods discussed above can be adapted to find the LCM of multiple numbers. For example, to find the LCM of 6, 11, and 15, you would first find the prime factorization of each number and then use the highest powers of each unique prime factor to calculate the LCM.
Furthermore, the concept of LCM is closely linked to other mathematical concepts such as the GCD, prime factorization, and modular arithmetic. A deep understanding of these concepts enhances the ability to solve more complex mathematical problems.
Conclusion: Mastering LCM Calculations
Understanding and calculating the least common multiple is a vital skill in mathematics. This guide has provided a comprehensive explanation of the concept, along with various methods for calculating the LCM, including the efficient prime factorization and GCD methods. We've also explored real-world applications of LCM, highlighting its importance in diverse fields. By mastering these techniques, you can confidently tackle LCM problems and utilize this fundamental mathematical concept to solve a wide range of mathematical and real-world challenges. Remember to practice regularly to improve your proficiency and speed in calculating LCMs. The more you practice, the more intuitive the process will become. And don't forget, the core concept remains the same, even as the numbers grow larger – finding the smallest positive integer that is evenly divisible by all the given numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 6 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.