What Is The Lcm Of 8 And 18
News Co
Mar 18, 2025 · 5 min read
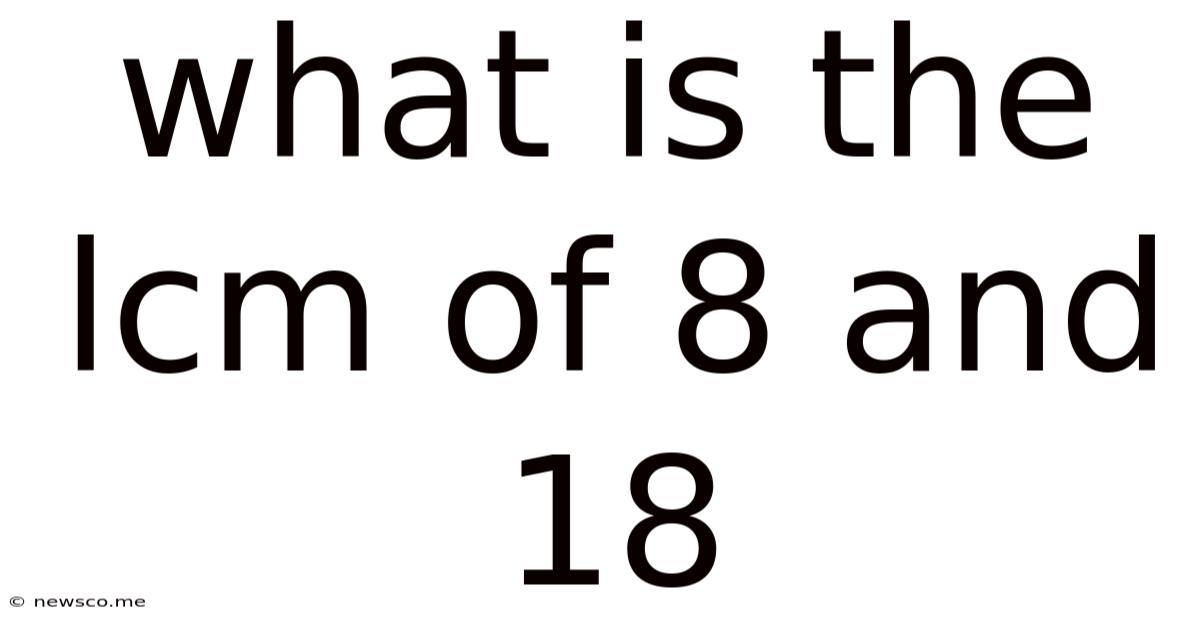
Table of Contents
What is the LCM of 8 and 18? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating the LCM opens doors to more complex mathematical applications. This comprehensive guide will not only answer the question "What is the LCM of 8 and 18?" but also delve into the broader world of LCMs, exploring different approaches and their practical uses.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that both (or all) of your starting numbers can divide into evenly. This concept is fundamental in various mathematical fields, including algebra, number theory, and even practical applications like scheduling and measurement conversions.
Key Concepts Related to LCM
Before diving into the calculation of the LCM of 8 and 18, let's solidify our understanding of a few key related concepts:
-
Multiples: A multiple of a number is the result of multiplying that number by any integer (positive, negative, or zero). For example, multiples of 8 include 8, 16, 24, 32, and so on.
-
Factors: Factors are numbers that divide another number exactly without leaving a remainder. For instance, the factors of 18 are 1, 2, 3, 6, 9, and 18.
-
Prime Factorization: This crucial concept involves breaking down a number into its prime factors—numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, etc.). Prime factorization is a powerful tool in calculating the LCM.
-
Greatest Common Divisor (GCD): The greatest common divisor (GCD) is the largest number that divides both (or all) of your starting numbers without leaving a remainder. The GCD and LCM are closely related, and knowing one can help you find the other.
Calculating the LCM of 8 and 18: Three Methods
Now, let's tackle the core question: what is the LCM of 8 and 18? We'll explore three common methods:
Method 1: Listing Multiples
This is the most straightforward, albeit potentially time-consuming, method, especially for larger numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
Multiples of 18: 18, 36, 54, 72, 90...
Notice that 72 appears in both lists. Therefore, the LCM of 8 and 18 is 72.
Method 2: Prime Factorization
This method leverages the power of prime factorization for a more efficient calculation, especially with larger numbers.
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 18 = 2 x 3 x 3 = 2 x 3²
-
Identify the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3² = 9
-
Multiply the highest powers together:
- LCM(8, 18) = 2³ x 3² = 8 x 9 = 72
This method is generally preferred for its efficiency and clarity.
Method 3: Using the GCD
The LCM and GCD are intimately related. We can utilize the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
-
Find the GCD of 8 and 18:
The factors of 8 are 1, 2, 4, 8. The factors of 18 are 1, 2, 3, 6, 9, 18. The greatest common factor is 2. Therefore, GCD(8, 18) = 2.
-
Apply the formula:
LCM(8, 18) = (8 x 18) / 2 = 144 / 2 = 72
Practical Applications of LCM
Understanding and calculating LCMs isn't just an academic exercise. It has numerous practical applications in various fields:
Scheduling and Time Management:
Imagine you have two tasks: one that repeats every 8 days and another that repeats every 18 days. The LCM (72 days) tells you when both tasks will coincide again, helping in efficient scheduling. This is useful in project planning, resource allocation, and even personal time management.
Measurement Conversions:
When dealing with different units of measurement, the LCM can help find the smallest common denominator for accurate conversions. For example, converting between fractions with different denominators requires finding the LCM of the denominators.
Music Theory:
In music theory, the LCM helps determine the least common multiple of note durations, essential for understanding rhythmic patterns and compositions.
Modular Arithmetic:
LCM plays a vital role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
Beyond the Basics: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly efficient in this case. For example, to find the LCM of 8, 18, and 12:
-
Prime Factorization:
- 8 = 2³
- 18 = 2 x 3²
- 12 = 2² x 3
-
Highest Powers:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3² = 9
-
Multiply:
- LCM(8, 18, 12) = 2³ x 3² = 8 x 9 = 72
Therefore, the LCM of 8, 18, and 12 is 72.
Conclusion: Mastering LCM Calculations
This in-depth exploration has not only provided the answer to "What is the LCM of 8 and 18?" (72) but also equipped you with a solid understanding of the underlying concepts and various methods for calculating LCMs, even for more than two numbers. By understanding these methods, you can approach various mathematical problems with confidence and apply this crucial concept to real-world scenarios in scheduling, measurement, and beyond. The ability to efficiently calculate the LCM is a valuable skill with broad applications, enhancing your mathematical proficiency and problem-solving abilities. Remember to choose the method that best suits the numbers you're working with—listing multiples is suitable for smaller numbers, while prime factorization is more efficient for larger numbers. Mastering LCM calculations opens doors to a deeper understanding of number theory and its practical applications.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.