What Is The Lcm Of 8 And 4
News Co
Mar 17, 2025 · 5 min read
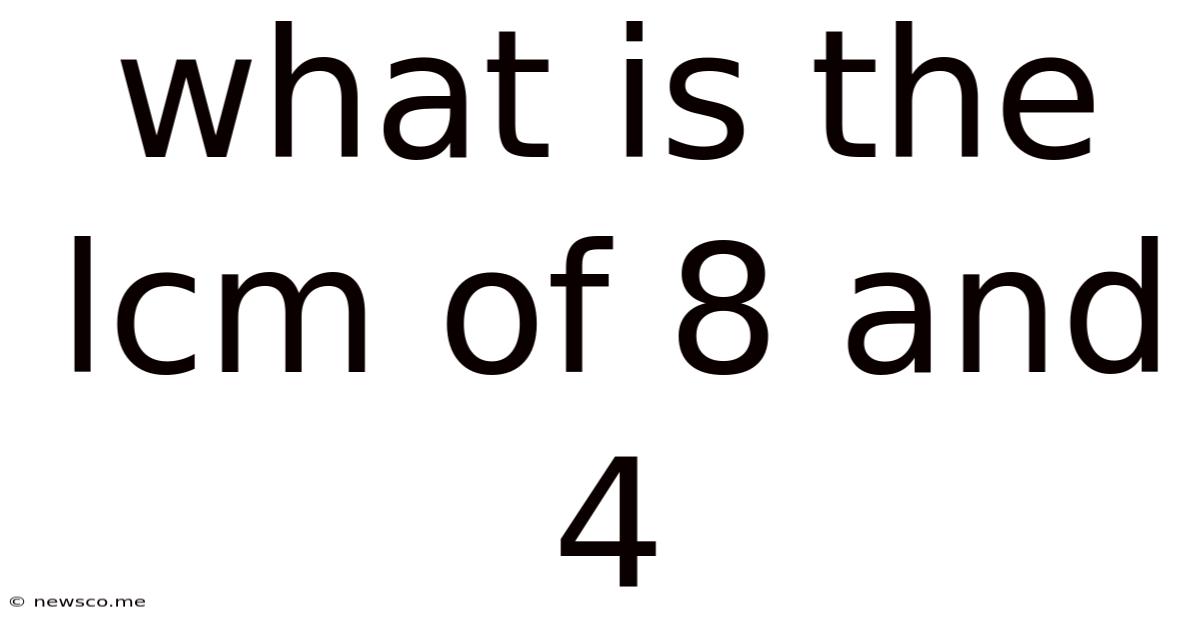
Table of Contents
What is the LCM of 8 and 4? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like algebra, number theory, and even practical applications involving scheduling and measurement. This article delves deep into determining the LCM of 8 and 4, exploring various methods, and extending the understanding to more complex scenarios. We'll also examine the broader context of LCMs and their significance.
Understanding Least Common Multiples (LCM)
Before tackling the specific problem of finding the LCM of 8 and 4, let's establish a solid foundation. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers in the set as factors.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The common multiples are 6, 12, 18... and the least common multiple is 6.
Method 1: Listing Multiples
The simplest method to find the LCM, especially for smaller numbers like 8 and 4, is to list the multiples of each number and identify the smallest common multiple.
Let's list the multiples of 8: 8, 16, 24, 32, 40, 48...
Now, let's list the multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32...
By comparing the two lists, we can easily see that the smallest common multiple is 8. Therefore, the LCM of 8 and 4 is 8.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves breaking down each number into its prime factors. Prime numbers are whole numbers greater than 1 that have only two divisors: 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Prime factorization of 8: 2 x 2 x 2 = 2³
Prime factorization of 4: 2 x 2 = 2²
To find the LCM using prime factorization, we take the highest power of each prime factor present in the numbers:
The only prime factor is 2, and the highest power is 2³ (from the factorization of 8).
Therefore, the LCM of 8 and 4 is 2³ = 8.
Method 3: Using the Formula (for two numbers)
There's a handy formula specifically for finding the LCM of two numbers, a and b:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where GCD(a, b) represents the greatest common divisor of a and b.
Let's apply this to our example:
- a = 8
- b = 4
First, we need to find the GCD of 8 and 4. The GCD is the largest number that divides both 8 and 4 without leaving a remainder. In this case, the GCD(8, 4) = 4.
Now, we can use the formula:
LCM(8, 4) = (|8 x 4|) / GCD(8, 4) = 32 / 4 = 8
The Relationship Between LCM and GCD
The LCM and GCD are intrinsically linked. Notice in the formula above how they are inversely related. For two numbers, their product is always equal to the product of their LCM and GCD:
a x b = LCM(a, b) x GCD(a, b)
This relationship is valuable because if you know one of these values (either the LCM or GCD), you can easily calculate the other.
Extending to More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply consider all prime factors from all numbers and take the highest power of each. For the listing multiples method, it becomes increasingly tedious as the number of integers grows.
Let's find the LCM of 8, 4, and 6:
Prime factorization:
- 8 = 2³
- 4 = 2²
- 6 = 2 x 3
The highest power of 2 is 2³ and the highest power of 3 is 3¹. Therefore, LCM(8, 4, 6) = 2³ x 3 = 8 x 3 = 24.
Real-World Applications of LCM
The concept of LCM isn't just confined to the realm of abstract mathematics. It has several practical applications:
- Scheduling: Imagine two buses that depart from a station at different intervals. The LCM helps determine when both buses will depart simultaneously again.
- Fractions: Finding the LCM of the denominators is essential when adding or subtracting fractions with different denominators.
- Measurement: When dealing with measurements in different units (e.g., converting inches to feet), LCM helps find the least common multiple to simplify calculations.
- Gear Ratios: In engineering, particularly in mechanics, understanding LCM is vital when designing gear systems to achieve specific speed or torque ratios.
- Music: The LCM plays a role in understanding musical intervals and harmonies.
Advanced Concepts and Further Exploration
For those interested in delving deeper, there are advanced concepts related to LCMs and their generalizations:
- Least Common Multiple of Polynomials: The concept extends to algebraic expressions, finding the LCM of polynomials.
- Algorithms for LCM Calculation: Efficient algorithms exist for computing the LCM of larger numbers, especially when dealing with thousands or even millions of numbers.
- Number Theory: The LCM plays a significant role in various branches of number theory, including modular arithmetic and Diophantine equations.
Conclusion
Finding the LCM of 8 and 4, while seemingly simple, serves as a gateway to understanding a powerful mathematical concept with significant applications across various fields. Through the various methods presented—listing multiples, prime factorization, and the formula—we've established a robust understanding of how to determine the LCM and its relationship with the GCD. Remember, mastering these fundamentals opens doors to tackling more complex mathematical problems and understanding real-world scenarios where the LCM plays a critical role. Whether you're a student working on your math homework or a professional applying these principles in your career, grasping the concept of LCM is undeniably valuable.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.