What Is The Lcm Of 9 And 15
News Co
Mar 27, 2025 · 5 min read
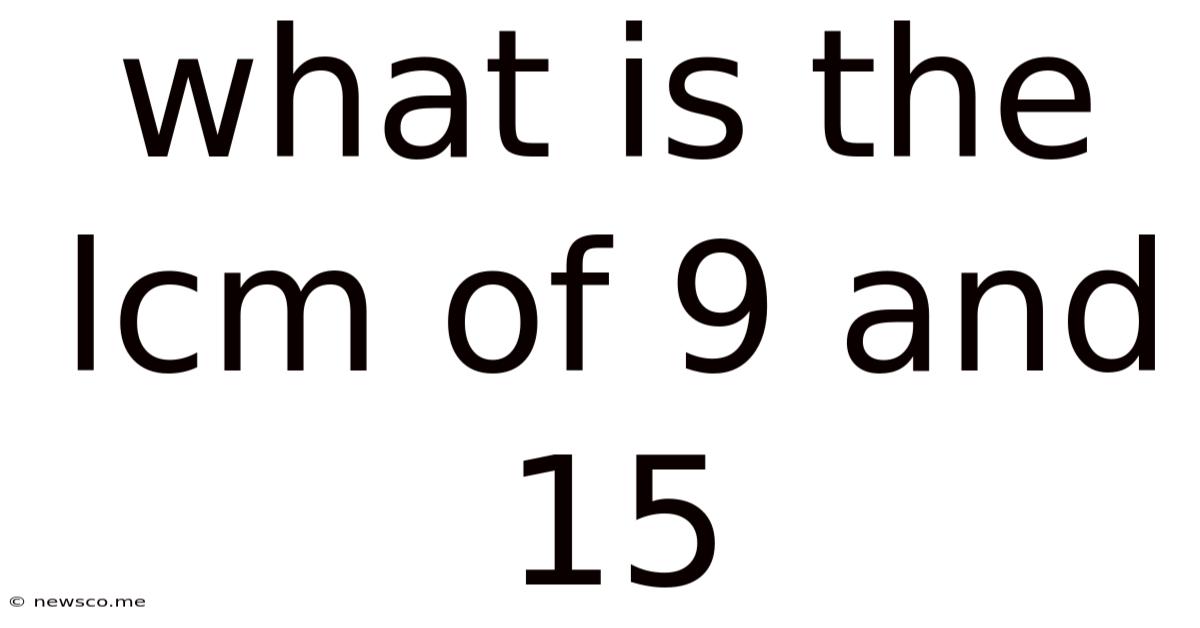
Table of Contents
What is the LCM of 9 and 15? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods for calculating the LCM is crucial for a strong foundation in mathematics. This comprehensive guide delves into the LCM of 9 and 15, exploring multiple approaches, explaining the reasoning behind each step, and highlighting the broader significance of LCMs in various mathematical applications.
Understanding Least Common Multiples (LCM)
Before we dive into finding the LCM of 9 and 15, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the prime factors of the original numbers.
Key characteristics of the LCM:
- Positive Integer: The LCM is always a positive whole number.
- Divisibility: It's perfectly divisible by each of the original numbers.
- Minimality: It's the smallest number that satisfies the divisibility condition.
Method 1: Listing Multiples
One of the simplest methods, especially for smaller numbers like 9 and 15, is to list the multiples of each number until you find the smallest common multiple.
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, ...
Multiples of 15: 15, 30, 45, 60, 75, 90, 105, ...
By comparing the lists, we observe that the smallest number appearing in both lists is 45. Therefore, the LCM of 9 and 15 is 45.
This method is straightforward and easy to visualize, but it can become cumbersome when dealing with larger numbers.
Method 2: Prime Factorization
A more efficient and systematic approach, especially for larger numbers, involves prime factorization. This method breaks down each number into its prime factors – the prime numbers that multiply to give the original number.
Prime factorization of 9: 3 x 3 = 3²
Prime factorization of 15: 3 x 5
To find the LCM using prime factorization:
- Identify the prime factors: We have 3 and 5.
- Find the highest power of each prime factor: The highest power of 3 is 3² (from the factorization of 9), and the highest power of 5 is 5¹ (from the factorization of 15).
- Multiply the highest powers: 3² x 5 = 9 x 5 = 45
Therefore, the LCM of 9 and 15 using prime factorization is 45. This method is more efficient and scalable for larger numbers.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the relationship between the LCM and GCD to calculate the LCM:
Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
Let's apply this method to find the LCM of 9 and 15:
-
Find the GCD of 9 and 15: The factors of 9 are 1, 3, and 9. The factors of 15 are 1, 3, 5, and 15. The greatest common factor is 3. Therefore, GCD(9, 15) = 3.
-
Apply the formula: LCM(9, 15) = (9 x 15) / 3 = 135 / 3 = 45
Therefore, the LCM of 9 and 15 using the GCD method is 45. This method is particularly useful when dealing with larger numbers where finding the prime factorization might be more challenging.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Scheduling: Imagine two buses depart from the same station, one every 9 minutes and the other every 15 minutes. The LCM (45 minutes) determines when both buses will depart simultaneously again. This is crucial for scheduling and coordinating events.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator, simplifying the calculation.
-
Construction and Engineering: In construction projects, LCM is used in calculating the optimal lengths of materials or determining cyclical patterns in construction processes.
-
Music Theory: LCM plays a role in understanding musical intervals and harmonies, determining when different musical phrases will align rhythmically.
-
Computer Science: LCM is utilized in algorithms and data structures, particularly in tasks related to synchronization and scheduling of processes.
Beyond the Basics: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. For prime factorization, you simply consider all the prime factors of all the numbers and take the highest power of each. For the GCD method, you can use iterative approaches to find the GCD of multiple numbers and then apply a similar formula to find the LCM.
Conclusion: The Significance of Understanding LCM
The seemingly simple task of finding the LCM of 9 and 15 opens a door to a deeper understanding of number theory and its practical applications. Mastering different methods for calculating the LCM empowers you to solve more complex problems in mathematics and various related fields. Whether you use the listing method, prime factorization, or the GCD method, understanding the underlying principles and choosing the most efficient method based on the numbers involved are key to success. The ability to confidently calculate LCMs demonstrates a solid grasp of fundamental mathematical concepts and equips you with valuable problem-solving skills. Remember, practice is key to mastering these techniques and applying them effectively in various scenarios. So, keep practicing and expanding your mathematical knowledge!
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 9 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.