What Is The Lcm Of 9 And 4
News Co
Apr 04, 2025 · 5 min read
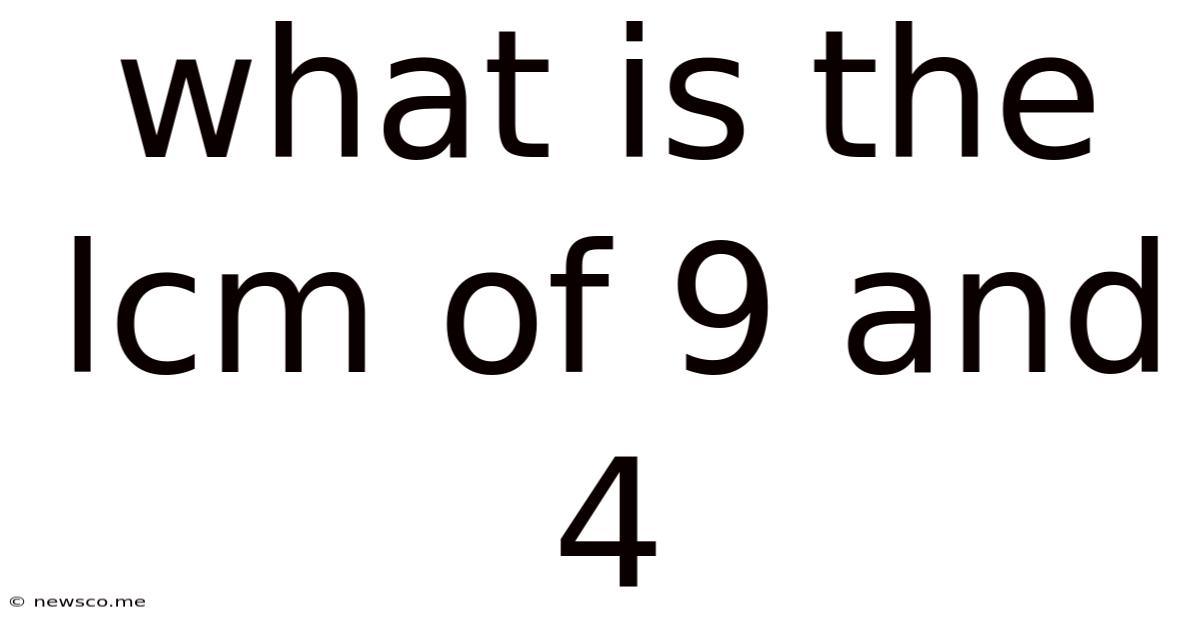
Table of Contents
What is the LCM of 9 and 4? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly important in areas like algebra, number theory, and even practical applications involving fractions and scheduling. This article delves deep into the question: What is the LCM of 9 and 4? We'll not only answer this specific question but also explore the various methods for calculating LCMs, highlighting their practical applications and theoretical underpinnings. We'll cover different approaches, from prime factorization to the Euclidean algorithm, ensuring a thorough understanding for all levels of mathematical proficiency.
Understanding Least Common Multiples (LCM)
Before we tackle the LCM of 9 and 4, let's solidify our understanding of the concept itself. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the integers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... Multiples of 3 are 3, 6, 9, 12, 15... The common multiples are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore the LCM of 2 and 3 is 6.
This seemingly simple concept has far-reaching implications in various mathematical and real-world scenarios.
Method 1: Prime Factorization to Find LCM(9, 4)
This method is often considered the most intuitive and efficient for finding the LCM of relatively small numbers. It involves breaking down each number into its prime factors.
Step 1: Prime Factorization of 9
9 can be expressed as the product of its prime factors: 3 x 3 = 3²
Step 2: Prime Factorization of 4
4 can be expressed as the product of its prime factors: 2 x 2 = 2²
Step 3: Identifying Common and Unique Prime Factors
We have the prime factors 2 and 3. Neither number shares any common prime factors.
Step 4: Calculating the LCM
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
In this case: 2² x 3² = 4 x 9 = 36
Therefore, the LCM of 9 and 4 is 36.
Method 2: Listing Multiples to Find LCM(9, 4)
This method, while less efficient for larger numbers, provides a clear visual understanding of the concept. It involves listing the multiples of each number until a common multiple is found.
Step 1: List Multiples of 9
9, 18, 27, 36, 45, 54, 63, 72...
Step 2: List Multiples of 4
4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
Step 3: Identify the Least Common Multiple
By comparing the lists, we see that the smallest common multiple is 36.
Therefore, the LCM of 9 and 4 is 36.
Method 3: Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder. We can use the Euclidean algorithm to find the GCD.
Step 1: Find the GCD of 9 and 4 using the Euclidean Algorithm
- Divide 9 by 4: 9 = 2 x 4 + 1
- Divide 4 by 1: 4 = 4 x 1 + 0
The last non-zero remainder is 1, so the GCD(9, 4) = 1.
Step 2: Apply the LCM Formula
LCM(9, 4) = (|9 x 4|) / GCD(9, 4) = 36 / 1 = 36
Therefore, the LCM of 9 and 4 is 36.
Real-World Applications of LCM
The LCM isn't just a theoretical concept; it has practical applications in various scenarios:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 9 minutes, and the other arrives every 4 minutes. The LCM (36 minutes) determines when both buses will arrive at the bus stop simultaneously.
-
Fractions: When adding or subtracting fractions, finding the LCM of the denominators is crucial to finding a common denominator for simplification.
-
Tiling and Patterns: In designing repeating patterns or tiling floors, the LCM helps determine the size of the repeating unit or the smallest tile that can seamlessly fit together.
-
Music Theory: The LCM is used in music theory to calculate the least common multiple of the durations of notes, enabling the creation of harmonious musical phrases.
-
Gear Ratios: In mechanical engineering, the LCM helps calculate gear ratios and the synchronization of rotating parts in machinery.
Further Exploration of LCM and Related Concepts
Understanding the LCM opens doors to a deeper understanding of related mathematical concepts:
-
Greatest Common Divisor (GCD): As demonstrated earlier, the GCD is intrinsically linked to the LCM. The relationship between the LCM and GCD is fundamental in number theory.
-
Euclidean Algorithm: This efficient algorithm for finding the GCD is a cornerstone of number theory and has wide-ranging applications in cryptography and computer science.
-
Modular Arithmetic: The concepts of LCM and GCD play a crucial role in modular arithmetic, which has applications in cryptography and computer science.
-
Number Theory: The study of LCM and GCD is integral to advanced number theory, encompassing topics like prime factorization and Diophantine equations.
Conclusion: The Power of the LCM
In conclusion, the least common multiple (LCM) of 9 and 4 is 36. We've explored three distinct methods to arrive at this answer, showcasing the versatility and practical importance of this fundamental mathematical concept. From prime factorization to the Euclidean algorithm and the formula relating LCM and GCD, we've touched upon the theoretical underpinnings and real-world applications of LCM, demonstrating its significance in diverse fields. Mastering the concept of LCM is not only beneficial for academic success but also for tackling various practical problems in everyday life and specialized fields. Understanding the different methods for calculating the LCM equips you with the tools to efficiently solve problems involving multiples and common factors, fostering a deeper appreciation for the elegance and practicality of mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 9 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.