What Is The Least Common Multiple Of 12 And 27
News Co
Mar 26, 2025 · 5 min read
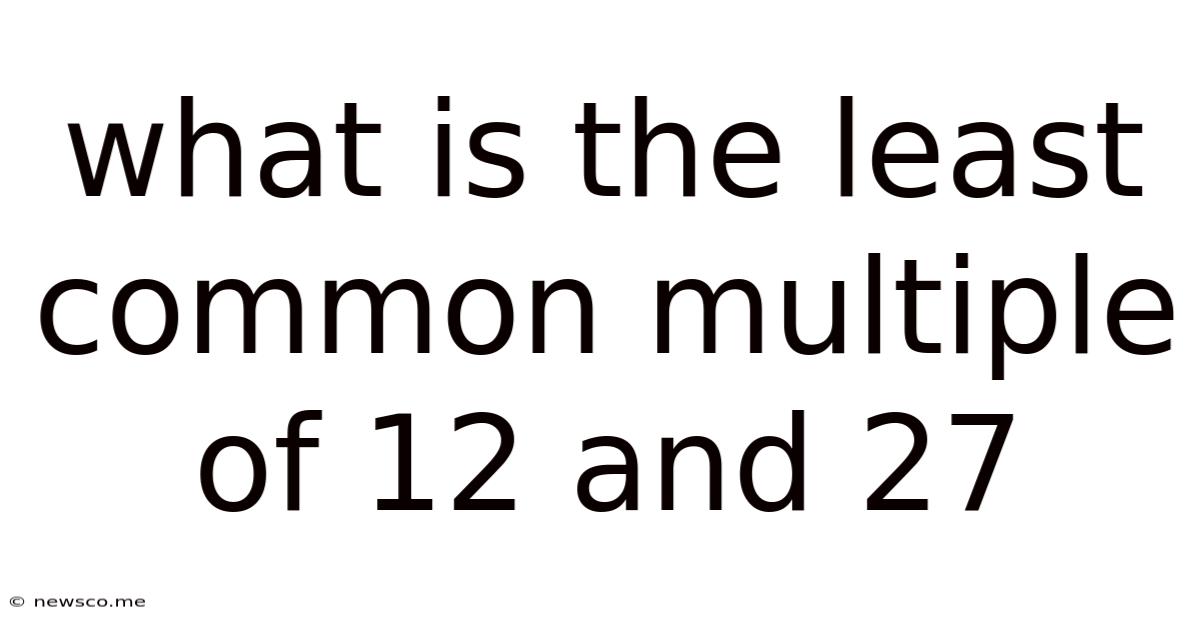
Table of Contents
What is the Least Common Multiple (LCM) of 12 and 27? A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic problem, but it's a fundamental concept in number theory with wide-ranging applications in mathematics, computer science, and beyond. This article will delve into the process of determining the LCM of 12 and 27, exploring different methods and offering a comprehensive understanding of the underlying principles. We’ll also examine the significance of LCM in various contexts and provide practical examples to solidify your understanding.
Understanding Least Common Multiples
Before we tackle the specific problem of finding the LCM of 12 and 27, let's establish a clear understanding of what a least common multiple actually is.
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
This concept is distinct from the greatest common divisor (GCD), which is the largest positive integer that divides each of the integers without leaving a remainder. While seemingly opposite, LCM and GCD are closely related, as we will see later.
Method 1: Listing Multiples
One straightforward method for finding the LCM is to list the multiples of each number until a common multiple is found. This method is particularly useful for smaller numbers.
Let's apply this to 12 and 27:
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
Multiples of 27: 27, 54, 81, 108, 135...
By comparing the lists, we observe that the smallest common multiple is 108. Therefore, the LCM(12, 27) = 108. This method works well for smaller numbers but becomes cumbersome and inefficient for larger numbers.
Method 2: Prime Factorization
A more efficient and systematic approach is to use prime factorization. This method involves breaking down each number into its prime factors. The LCM is then constructed using the highest power of each prime factor present in the factorization of either number.
Let's factorize 12 and 27:
- 12 = 2² × 3
- 27 = 3³
Now, let's identify the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3³ = 27
To find the LCM, we multiply these highest powers together:
LCM(12, 27) = 2² × 3³ = 4 × 27 = 108
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the GCD
The LCM and GCD are intimately related through the following formula:
LCM(a, b) × GCD(a, b) = a × b
This means that if we know the GCD of two numbers, we can easily calculate their LCM.
First, let's find the GCD of 12 and 27 using the Euclidean algorithm:
- Divide the larger number (27) by the smaller number (12): 27 ÷ 12 = 2 with a remainder of 3.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (3): 12 ÷ 3 = 4 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 3.
Therefore, GCD(12, 27) = 3.
Now, we can use the formula:
LCM(12, 27) = (12 × 27) / GCD(12, 27) = (12 × 27) / 3 = 324 / 3 = 108
This method provides another efficient way to calculate the LCM, especially when the GCD is easily determined.
Applications of LCM
The concept of LCM has numerous applications across various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if one bus arrives every 12 minutes and another every 27 minutes, the LCM (108 minutes) tells us when they'll arrive at the same stop together.
-
Fractions: Finding the least common denominator when adding or subtracting fractions. This simplifies the process significantly.
-
Music Theory: Calculating the least common multiple of the frequencies of different notes to find the period of a musical phrase.
-
Computer Science: Optimizing algorithms and data structures, especially in areas like scheduling and synchronization.
-
Engineering: In designing systems where components operate at different cycles or frequencies.
-
Everyday Life: In simple tasks such as dividing food equally among groups, or in organizing schedules.
Further Exploration: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you simply consider the highest power of each prime factor present in any of the factorizations. For the GCD-based method, you can iteratively apply the process, finding the LCM of two numbers at a time, until you've included all the numbers.
Conclusion: The Significance of LCM(12, 27) = 108
Throughout this in-depth exploration, we've definitively established that the least common multiple of 12 and 27 is 108. We've examined three distinct methods – listing multiples, prime factorization, and the GCD method – each offering unique insights and advantages depending on the context and the size of the numbers involved. Understanding these methods provides a solid foundation in number theory and equips you to tackle more complex problems involving LCM calculations. Furthermore, the diverse applications of LCM highlighted demonstrate its pervasive importance in various fields, reinforcing its fundamental role in mathematics and beyond. By grasping these concepts, you'll be better equipped to solve real-world problems and enhance your understanding of mathematical principles. Remember, mastering LCM is not just about calculating a single answer; it's about understanding the underlying concepts and their practical implications.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 12 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.