What Is The Least Common Multiple Of 12 And 36
News Co
Mar 31, 2025 · 4 min read
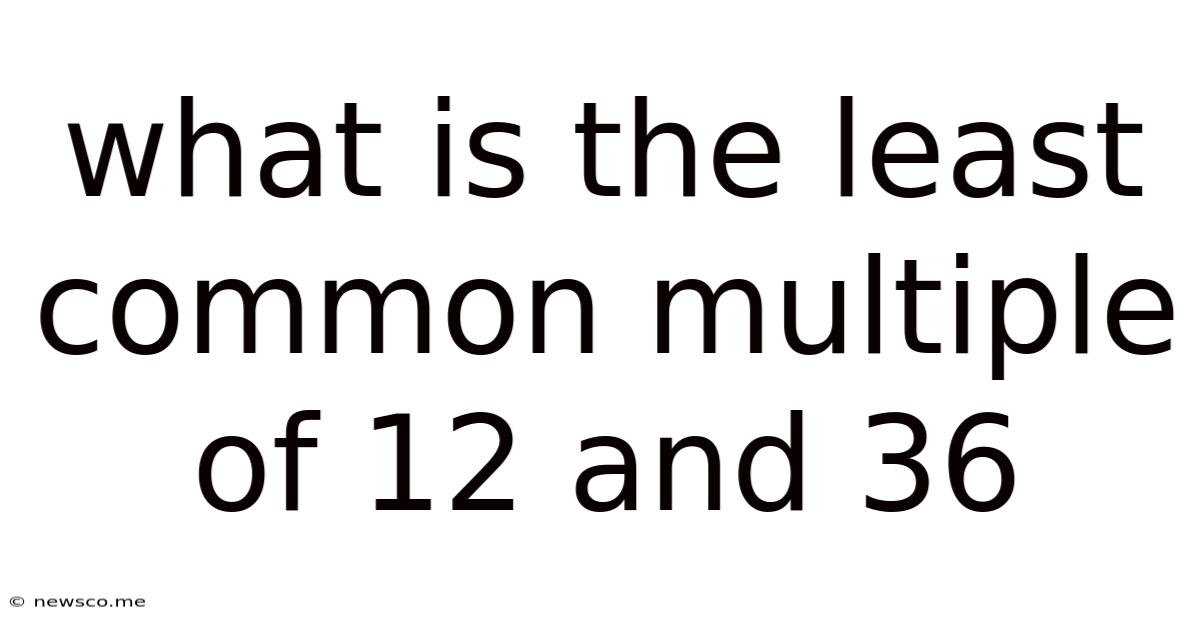
Table of Contents
What is the Least Common Multiple (LCM) of 12 and 36? A Deep Dive into Finding LCMs
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex equations in algebra and beyond. This comprehensive guide will thoroughly explore how to determine the LCM of 12 and 36, employing multiple methods to solidify understanding and showcasing the broader implications of LCM calculations. We'll also delve into the practical uses of LCMs in everyday life and more advanced mathematical contexts.
Understanding Least Common Multiples
Before diving into the specific calculation for 12 and 36, let's clarify the definition of a least common multiple. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the integers as factors.
For example, consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20, 24... The multiples of 6 are 6, 12, 18, 24, 30... The common multiples are 12, 24, 36... The least common multiple is 12.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers like 12 and 36. We simply list the multiples of each number until we find the smallest common multiple.
Multiples of 12: 12, 24, 36, 48, 60, 72...
Multiples of 36: 36, 72, 108, 144...
By comparing the lists, we see that the smallest number appearing in both lists is 36. Therefore, the LCM of 12 and 36 is 36.
This method is effective for smaller numbers but becomes cumbersome and inefficient for larger numbers. Let's explore more efficient methods.
Method 2: Prime Factorization
This is a more robust and efficient method, particularly useful for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Prime Factorization of 12:
12 = 2 x 2 x 3 = 2² x 3¹
Prime Factorization of 36:
36 = 2 x 2 x 3 x 3 = 2² x 3²
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
Now, multiply these highest powers together:
LCM(12, 36) = 2² x 3² = 4 x 9 = 36
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers with multiple prime factors.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are closely related. There's a formula that links them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 12 and 36 using the Euclidean algorithm:
- Divide the larger number (36) by the smaller number (12): 36 ÷ 12 = 3 with a remainder of 0.
- Since the remainder is 0, the GCD is the smaller number, which is 12.
Now, apply the formula:
LCM(12, 36) x GCD(12, 36) = 12 x 36
LCM(12, 36) x 12 = 432
LCM(12, 36) = 432 ÷ 12 = 36
This method is also efficient and highlights the relationship between LCM and GCD.
Applications of LCMs
Understanding and calculating LCMs has widespread applications across various fields:
1. Fraction Arithmetic:
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/12 and 1/36, the LCM of 12 and 36 (which is 36) becomes the common denominator.
2. Scheduling Problems:
LCMs are crucial in solving scheduling problems. For example, if two buses depart from a station at different intervals (say, Bus A every 12 minutes and Bus B every 36 minutes), the LCM helps determine when both buses will depart simultaneously again. In this case, they'll depart together every 36 minutes.
3. Gear Ratios and Engineering:
In mechanical engineering, LCMs are used in calculating gear ratios and determining the synchronization of rotating components in machinery.
4. Music Theory:
In music theory, LCMs help determine the least common denominator for different rhythmic patterns or time signatures.
5. Modular Arithmetic and Cryptography:
LCMs play a vital role in modular arithmetic, a branch of number theory used extensively in cryptography for encryption and decryption algorithms.
Conclusion: Mastering LCM Calculations
Determining the least common multiple of 12 and 36, as demonstrated, is achievable through various methods. While listing multiples is suitable for smaller numbers, prime factorization and the GCD method prove far more efficient for larger numbers and more complex problems. Understanding LCMs isn't just about solving mathematical puzzles; it's a fundamental skill with practical applications in numerous fields. Mastering these techniques empowers you to tackle more complex mathematical problems and appreciate the interconnectedness of mathematical concepts. The ability to efficiently calculate LCMs is a valuable asset, opening doors to a deeper understanding of mathematics and its practical applications in the real world. Further exploration into these methods and their applications will solidify your understanding and equip you with valuable problem-solving skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 12 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.