What Is The Least Common Multiple Of 15 And 30
News Co
Apr 03, 2025 · 5 min read
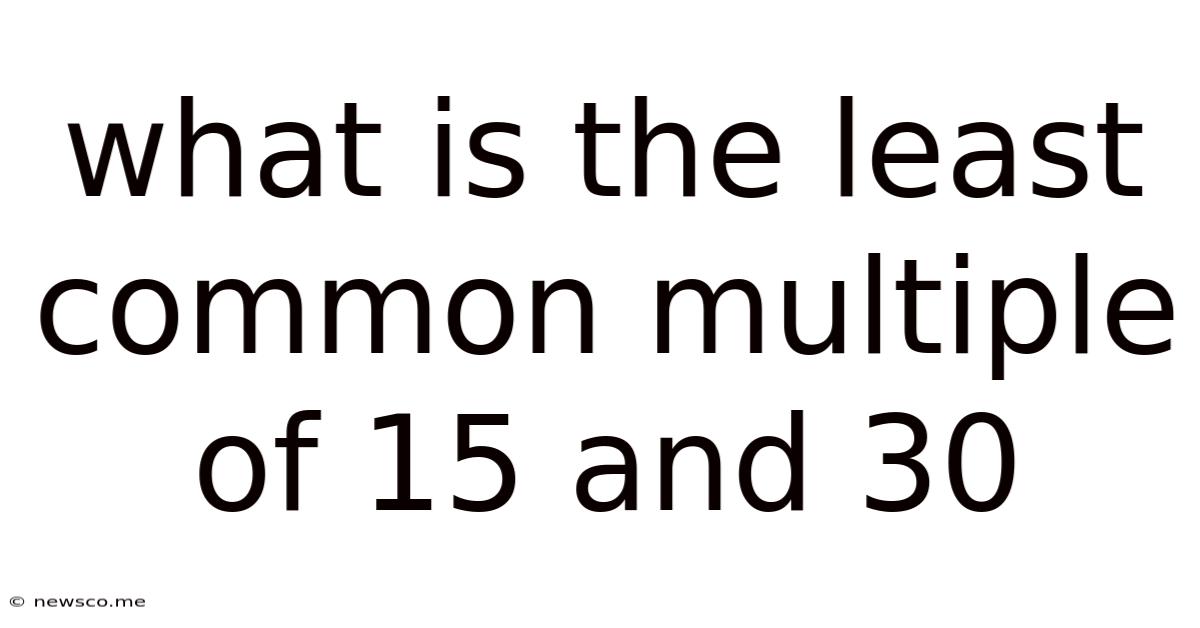
Table of Contents
What is the Least Common Multiple (LCM) of 15 and 30? A Deep Dive into Finding LCMs
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and even music theory. This article will delve into the methods of calculating the LCM, focusing specifically on the LCM of 15 and 30, but also providing a broader understanding applicable to a wide range of numbers. We'll explore different approaches, from the straightforward listing method to more advanced techniques like prime factorization and the greatest common divisor (GCD) method. By the end, you'll not only know the LCM of 15 and 30 but also possess a comprehensive toolkit for tackling any LCM problem.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. Think of it as the smallest common "target" number that all the numbers can reach through multiplication.
For instance, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... The multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. Let's apply it to find the LCM of 15 and 30:
1. List the multiples of 15: 15, 30, 45, 60, 75, 90, 105...
2. List the multiples of 30: 30, 60, 90, 120, 150...
3. Identify the smallest common multiple: The smallest number appearing in both lists is 30.
Therefore, the LCM of 15 and 30 is 30.
Method 2: Prime Factorization
Prime factorization is a more powerful method, particularly useful for larger numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
1. Find the prime factorization of 15: 15 = 3 x 5
2. Find the prime factorization of 30: 30 = 2 x 3 x 5
3. Identify the highest power of each prime factor: The prime factors involved are 2, 3, and 5. The highest power of 2 is 2¹, the highest power of 3 is 3¹, and the highest power of 5 is 5¹.
4. Multiply the highest powers together: 2¹ x 3¹ x 5¹ = 30
Therefore, the LCM of 15 and 30 is 30.
Method 3: Using the Greatest Common Divisor (GCD)
The GCD is the largest number that divides both given numbers without leaving a remainder. There's a handy relationship between the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
1. Find the GCD of 15 and 30: The divisors of 15 are 1, 3, 5, and 15. The divisors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30. The greatest common divisor is 15.
2. Apply the formula: LCM(15, 30) x GCD(15, 30) = 15 x 30
3. Solve for LCM: LCM(15, 30) x 15 = 450 => LCM(15, 30) = 450 / 15 = 30
Therefore, the LCM of 15 and 30 is 30.
Why is the LCM important?
Understanding LCM is crucial for various mathematical operations and real-world applications:
1. Fraction Addition and Subtraction:
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/15 and 1/30, you need to find the LCM of 15 and 30 (which is 30), convert the fractions to have a common denominator, and then add the numerators.
2. Solving Problems Involving Cycles or Periods:
Imagine two machines running cycles at different intervals. One machine completes a cycle every 15 seconds, and another every 30 seconds. To determine when both machines will complete a cycle simultaneously, you need to find the LCM of 15 and 30. The answer, 30 seconds, tells us they'll both complete a cycle together after 30 seconds.
3. Music Theory:
Musical intervals and harmony are often expressed in terms of ratios of frequencies. LCM plays a role in understanding when different musical notes or chords will align harmoniously.
4. Scheduling and Time Management:
Imagine planning events that recur at different intervals (e.g., meetings every 15 days and another every 30 days). Finding the LCM helps determine when both events will coincide.
Advanced Techniques for Finding LCMs
For larger sets of numbers or numbers with many factors, more advanced algorithms become necessary. These often utilize the prime factorization method combined with efficient computational techniques. However, for the relatively small numbers like 15 and 30, the methods described earlier are sufficient and easy to understand.
Conclusion: The LCM of 15 and 30 is 30
We've explored various methods to determine the least common multiple of 15 and 30, consistently arriving at the answer: 30. This exploration not only solidified the understanding of LCM for this specific pair of numbers but also equipped you with a comprehensive understanding of the concept and multiple methods for calculating the LCM of any set of numbers. Remember to choose the method that best suits the complexity of the numbers you're working with. The listing method is intuitive for small numbers, while prime factorization becomes more efficient for larger ones. Understanding the relationship between LCM and GCD provides another valuable tool in your mathematical toolkit. This comprehensive understanding of LCM lays the foundation for more advanced mathematical concepts and problem-solving skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 15 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.