What Is The Least Common Multiple Of 15 And 40
News Co
Apr 03, 2025 · 6 min read
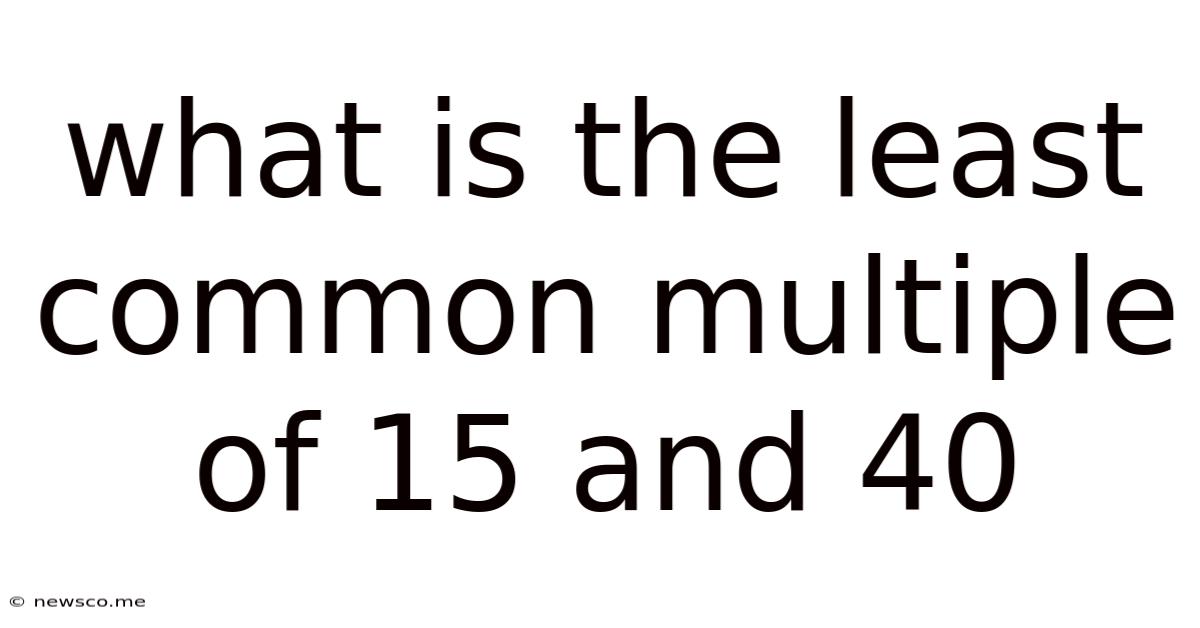
Table of Contents
Unraveling the Least Common Multiple (LCM) of 15 and 40: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods offers valuable insights into number theory and its practical applications. This comprehensive guide delves into the intricacies of calculating the LCM of 15 and 40, exploring various approaches and highlighting their relevance in diverse mathematical contexts. We’ll move beyond a simple answer and uncover the rich mathematical landscape surrounding this seemingly basic calculation.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 15 and 40, let's establish a firm understanding of what an LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly.
This concept has wide-ranging applications, extending far beyond simple arithmetic exercises. For instance, LCMs are crucial in:
- Scheduling: Determining when events that occur at different intervals will coincide (e.g., two buses arriving at a stop at different frequencies).
- Fraction Operations: Finding a common denominator when adding or subtracting fractions.
- Music Theory: Calculating rhythmic patterns and harmonies.
- Engineering: Synchronizing mechanical systems with varying cycles.
Understanding LCMs provides a fundamental building block for solving a variety of problems across multiple disciplines.
Method 1: Listing Multiples
The most straightforward, albeit sometimes tedious, method for finding the LCM is by listing the multiples of each number until a common multiple is found.
Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150...
Multiples of 40: 40, 80, 120, 160, 200, 240...
By comparing the lists, we observe that the smallest common multiple of 15 and 40 is 120. This method is effective for smaller numbers but becomes impractical for larger numbers or when dealing with multiple numbers simultaneously.
Method 2: Prime Factorization
A more efficient and elegant method for calculating the LCM involves prime factorization. This approach leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Let's break down 15 and 40 into their prime factors:
- 15 = 3 × 5
- 40 = 2³ × 5
To find the LCM, we take the highest power of each prime factor present in the factorization of either number and multiply them together:
LCM(15, 40) = 2³ × 3 × 5 = 8 × 3 × 5 = 120
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are intimately related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers themselves. This relationship provides an alternative method for calculating the LCM.
First, let's find the GCD of 15 and 40 using the Euclidean algorithm:
- Divide 40 by 15: 40 = 2 × 15 + 10
- Divide 15 by the remainder 10: 15 = 1 × 10 + 5
- Divide 10 by the remainder 5: 10 = 2 × 5 + 0
The last non-zero remainder is 5, so the GCD(15, 40) = 5.
Now, we can use the relationship between LCM and GCD:
LCM(15, 40) = (15 × 40) / GCD(15, 40) = (600) / 5 = 120
Comparing the Methods
Each method offers a unique approach to calculating the LCM. The method of listing multiples is intuitive but becomes cumbersome for larger numbers. Prime factorization is generally more efficient, especially for larger numbers, providing a systematic and elegant solution. The GCD method offers an alternative approach that leverages the inherent relationship between LCM and GCD. The best method to use often depends on the specific numbers involved and the available tools.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond abstract mathematical exercises. Let’s explore some practical applications:
-
Concert Scheduling: Imagine two bands are scheduled to perform at a music festival. Band A performs every 30 minutes, and Band B performs every 45 minutes. To find out when both bands will perform simultaneously, we need to find the LCM of 30 and 45, which is 90 minutes. This means both bands will perform together after 1 hour and 30 minutes.
-
Factory Production: A factory produces two types of widgets. Widget A is produced every 15 minutes, and Widget B is produced every 20 minutes. To determine when both widgets will be produced simultaneously, we need to calculate the LCM of 15 and 20, which is 60 minutes. The factory will produce both widgets simultaneously every hour.
-
Traffic Light Synchronization: Imagine two intersections with traffic lights. One light cycle is 60 seconds, and the other is 75 seconds. To synchronize the lights, ensuring both lights turn green simultaneously at regular intervals, we would need to find the LCM of 60 and 75.
-
Recipe Scaling: Consider a recipe that requires 15 ounces of ingredient A and 40 ounces of ingredient B. If you want to scale the recipe up while maintaining the same proportions, you need to find a common multiple of 15 and 40. Using the LCM (120), you could scale the recipe to use 120 ounces of ingredient A and 320 ounces of ingredient B.
Beyond the Basics: Extending the Concept
The concept of LCM isn’t limited to just two numbers. We can extend it to find the LCM of three or more numbers. The prime factorization method remains particularly useful in this context. For example, to find the LCM of 15, 40, and 21:
-
Prime Factorize each number:
- 15 = 3 × 5
- 40 = 2³ × 5
- 21 = 3 × 7
-
Identify the highest power of each prime factor: 2³, 3, 5, 7
-
Multiply the highest powers together: 2³ × 3 × 5 × 7 = 840
Therefore, the LCM(15, 40, 21) = 840.
Conclusion: The Power of LCM
The calculation of the least common multiple, while seemingly straightforward, reveals a depth of mathematical understanding with practical applications across various fields. From simplifying fractions to synchronizing complex systems, the LCM provides a fundamental tool for problem-solving. By mastering the different methods for calculating the LCM, you unlock a key to understanding and manipulating numerical relationships in a more efficient and insightful manner. The seemingly simple problem of finding the LCM of 15 and 40 serves as a gateway to a rich and rewarding exploration of number theory and its real-world relevance. Remember to choose the most suitable method based on the complexity of the numbers involved and your comfort level with different mathematical techniques. This comprehensive understanding empowers you to confidently tackle a wider range of mathematical challenges and appreciate the interconnectedness of seemingly disparate mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 15 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.