What Is The Least Common Multiple Of 15 And 9
News Co
Mar 22, 2025 · 5 min read
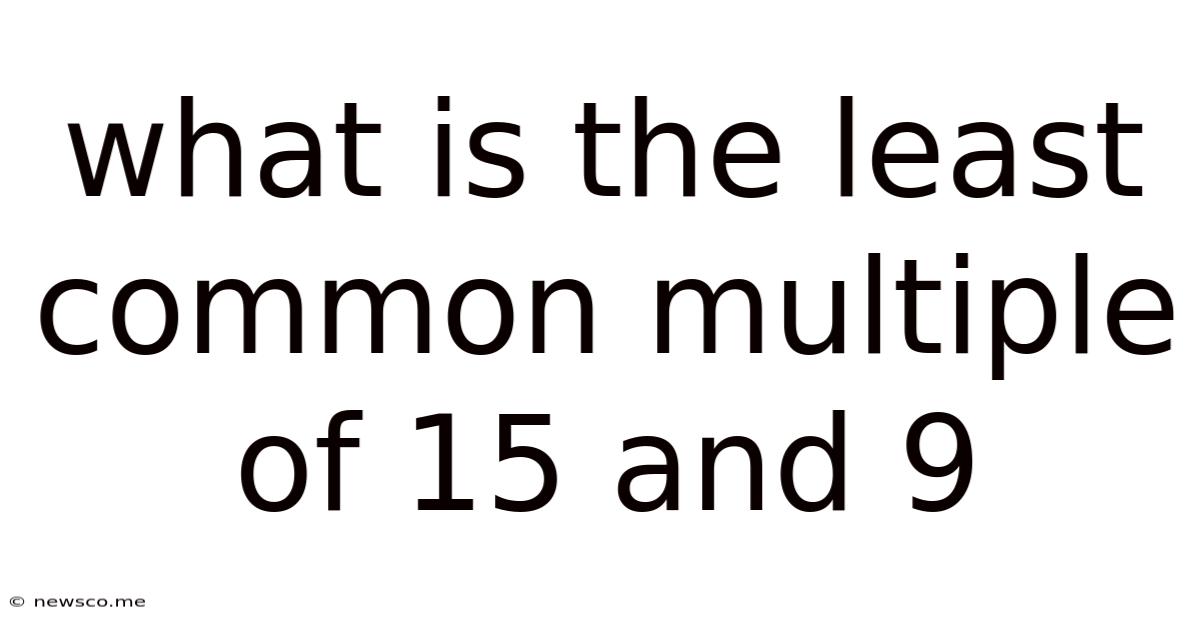
Table of Contents
What is the Least Common Multiple (LCM) of 15 and 9? A Deep Dive into Finding LCMs
Finding the least common multiple (LCM) might seem like a simple mathematical task, especially for smaller numbers like 15 and 9. However, understanding the underlying concepts and exploring different methods for calculating LCMs opens up a world of mathematical understanding applicable to various fields. This article delves into the intricacies of finding the LCM of 15 and 9, providing multiple approaches and highlighting the importance of LCMs in broader mathematical contexts.
Understanding Least Common Multiples (LCMs)
Before jumping into the calculation, let's solidify our understanding of LCMs. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors. For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24...
The common multiples are 6, 12, 18, and so on. The least common multiple, therefore, is 6.
This concept extends to more than two numbers. The LCM is a fundamental concept in mathematics with applications in various areas, including:
- Fractions: Finding a common denominator when adding or subtracting fractions.
- Scheduling: Determining when events will coincide (e.g., buses arriving at a stop).
- Music Theory: Understanding rhythmic relationships and harmonies.
- Computer Science: Algorithms and data structures.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers like 15 and 9, is to list their multiples until a common multiple is found.
Finding Multiples of 15:
15, 30, 45, 60, 75, 90, 105, 120...
Finding Multiples of 9:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108...
By comparing the lists, we can see that the smallest common multiple is 45.
This method is simple and intuitive but can become inefficient when dealing with larger numbers or multiple numbers.
Method 2: Prime Factorization
A more efficient and robust method is to use prime factorization. This method involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Prime Factorization of 15:
15 = 3 x 5
Prime Factorization of 9:
9 = 3 x 3 = 3²
Now, we construct the LCM by taking the highest power of each prime factor present in the factorizations:
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
Therefore, the LCM of 15 and 9 is 9 x 5 = 45.
This method is superior to listing multiples, particularly when dealing with larger numbers, as it provides a systematic and efficient approach. It avoids the tedious process of listing potentially numerous multiples.
Method 3: Using the Formula (LCM and GCD Relationship)
The least common multiple (LCM) and the greatest common divisor (GCD) are intimately related. There's a formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
Where 'a' and 'b' are the two numbers.
First, we need to find the greatest common divisor (GCD) of 15 and 9. The GCD is the largest number that divides both 15 and 9 without leaving a remainder. We can find this using the Euclidean algorithm or by listing the divisors:
Divisors of 15: 1, 3, 5, 15
Divisors of 9: 1, 3, 9
The greatest common divisor is 3.
Now, using the formula:
LCM(15, 9) * GCD(15, 9) = 15 * 9
LCM(15, 9) * 3 = 135
LCM(15, 9) = 135 / 3 = 45
This method provides a concise and mathematically elegant way to calculate the LCM, especially when the GCD is easily determined.
Understanding the Significance of LCM
The concept of the least common multiple extends far beyond simple mathematical exercises. It has significant implications across numerous fields:
1. Fraction Operations:
Adding or subtracting fractions requires a common denominator. This common denominator is the LCM of the denominators of the fractions. For example, to add 1/15 and 1/9, we need to find the LCM of 15 and 9, which is 45. We then rewrite the fractions with a denominator of 45 before performing the addition.
2. Cyclic Events:
LCMs are crucial in solving problems involving cyclic events. Imagine two buses, one arriving every 15 minutes and the other every 9 minutes. The LCM (45 minutes) tells us how long it will take for both buses to arrive at the stop simultaneously.
3. Music Theory:
In music, the LCM is used to determine the least common multiple of different rhythmic durations. This helps composers and musicians understand rhythmic relationships and create harmonious compositions.
4. Scheduling and Project Management:
In project management, LCM is used to synchronize tasks that are periodic in nature.
5. Computer Science Algorithms:
LCMs play a role in various computer science algorithms, particularly those dealing with number theory and data structures.
Conclusion: The LCM of 15 and 9 and Beyond
We've explored various methods to determine the least common multiple of 15 and 9, concluding that the LCM is 45. We've demonstrated three different approaches: listing multiples, prime factorization, and using the relationship between LCM and GCD. The choice of method depends on the complexity of the numbers involved. While listing multiples is suitable for smaller numbers, prime factorization and the LCM-GCD relationship offer more efficient and scalable solutions for larger numbers. However, understanding the fundamental concept of LCM and its wide-ranging applications remains the key takeaway. The seemingly simple calculation of the LCM of 15 and 9 serves as a gateway to appreciating the power and versatility of this fundamental mathematical concept. It underscores its importance in various fields and encourages further exploration of related mathematical principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 15 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.