What Is The Least Common Multiple Of 18 And 45
News Co
Apr 16, 2025 · 4 min read
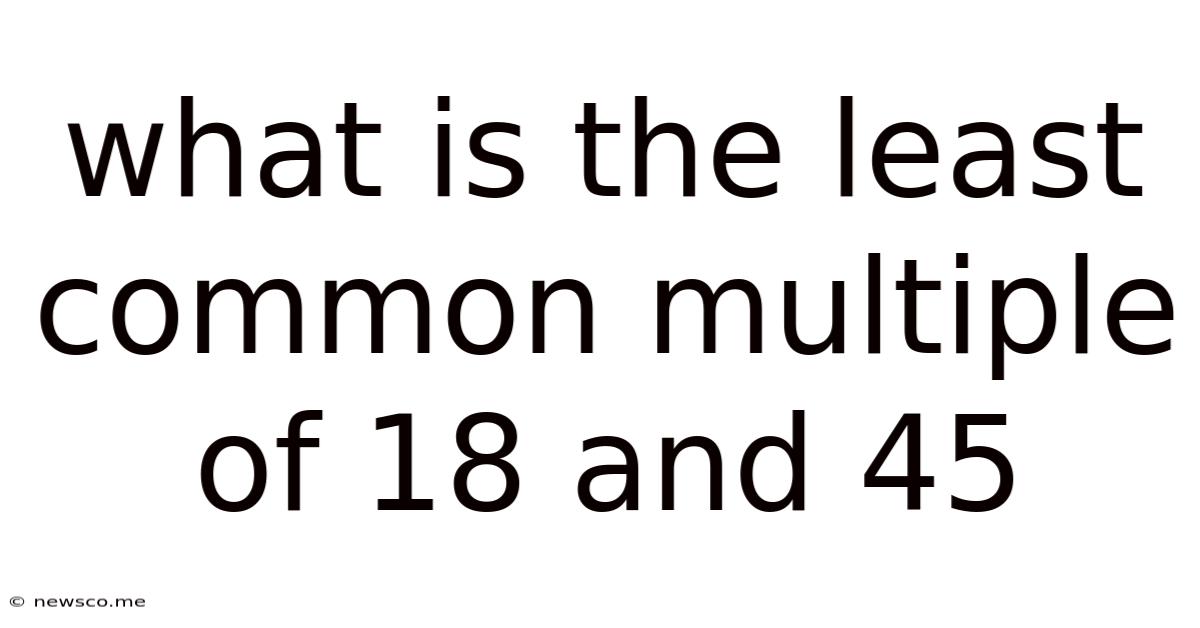
Table of Contents
What is the Least Common Multiple (LCM) of 18 and 45? A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem like a simple arithmetic problem, but understanding its underlying principles unlocks a deeper appreciation for number theory and its applications in various fields. This article will explore the LCM of 18 and 45 in detail, explaining multiple methods for calculation, highlighting its significance, and providing real-world examples.
Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the integers as factors. This concept is crucial in various mathematical contexts, from simplifying fractions to solving problems involving cyclical events.
Methods for Finding the LCM of 18 and 45
Several methods can efficiently determine the LCM of 18 and 45. Let's explore the most common approaches:
1. Listing Multiples Method
This method, while straightforward, can be time-consuming for larger numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180...
- Multiples of 45: 45, 90, 135, 180, 225...
The smallest multiple common to both lists is 90. Therefore, the LCM(18, 45) = 90.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. We find the prime factorization of each number and then construct the LCM using the highest powers of each prime factor present.
- Prime factorization of 18: 2 x 3²
- Prime factorization of 45: 3² x 5
To find the LCM, we take the highest power of each prime factor present in either factorization: 2¹, 3², and 5¹.
LCM(18, 45) = 2¹ x 3² x 5¹ = 2 x 9 x 5 = 90
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The product of the LCM and GCD of two numbers is equal to the product of the two numbers.
Finding the GCD of 18 and 45 using the Euclidean Algorithm:
- Divide the larger number (45) by the smaller number (18): 45 ÷ 18 = 2 with a remainder of 9.
- Replace the larger number with the smaller number (18) and the smaller number with the remainder (9): 18 ÷ 9 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 9.
Now, we can use the formula: LCM(a, b) = (a x b) / GCD(a, b)
LCM(18, 45) = (18 x 45) / 9 = 810 / 9 = 90
Significance of the LCM
The concept of the least common multiple extends far beyond simple arithmetic exercises. It finds application in various fields:
1. Fraction Simplification
When adding or subtracting fractions, finding the LCM of the denominators is crucial for finding a common denominator. This simplifies the calculation significantly.
For example, adding 1/18 and 1/45:
The LCM of 18 and 45 is 90. We rewrite the fractions with the common denominator:
(5/90) + (2/90) = 7/90
2. Cyclical Events
The LCM is essential for solving problems involving cyclical events that repeat at different intervals. For example:
-
Scenario: Two clocks, one chiming every 18 seconds and the other every 45 seconds, chime simultaneously. When will they chime together again?
-
Solution: The time until they chime together again is the LCM of 18 and 45, which is 90 seconds.
3. Scheduling and Planning
In project management and scheduling, determining when tasks with different completion cycles will align often requires calculating the LCM. This helps in optimizing resource allocation and coordinating activities efficiently.
4. Music Theory
The LCM plays a role in music theory, particularly in determining when different musical patterns or rhythms will coincide.
5. Computer Science
In computer algorithms and data structures, the concept of LCM finds use in various optimization problems and synchronization techniques.
Beyond the Basics: Extending the LCM Concept
The LCM concept extends easily to more than two numbers. To find the LCM of multiple numbers, you can use the prime factorization method. Factorize each number into its prime factors, and then take the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to find the LCM.
For example, to find the LCM of 18, 45, and 30:
- 18 = 2 x 3²
- 45 = 3² x 5
- 30 = 2 x 3 x 5
The LCM(18, 45, 30) = 2¹ x 3² x 5¹ = 90
Conclusion: The Practical Power of the LCM
The seemingly simple concept of the least common multiple has significant implications across diverse fields. Understanding the different methods for calculating the LCM, along with its practical applications, equips you with a valuable tool for solving problems in mathematics, science, and beyond. This deep dive into the LCM of 18 and 45 provides not just the answer (90), but also a comprehensive understanding of its underlying principles and real-world relevance. Mastering the LCM is a key step in developing stronger mathematical reasoning and problem-solving skills. From simplifying fractions to synchronizing events, the LCM's importance is undeniable. By grasping its significance, you'll be better equipped to tackle a wider range of complex numerical challenges.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 18 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.