What Is The Least Common Multiple Of 20 And 40
News Co
Mar 25, 2025 · 5 min read
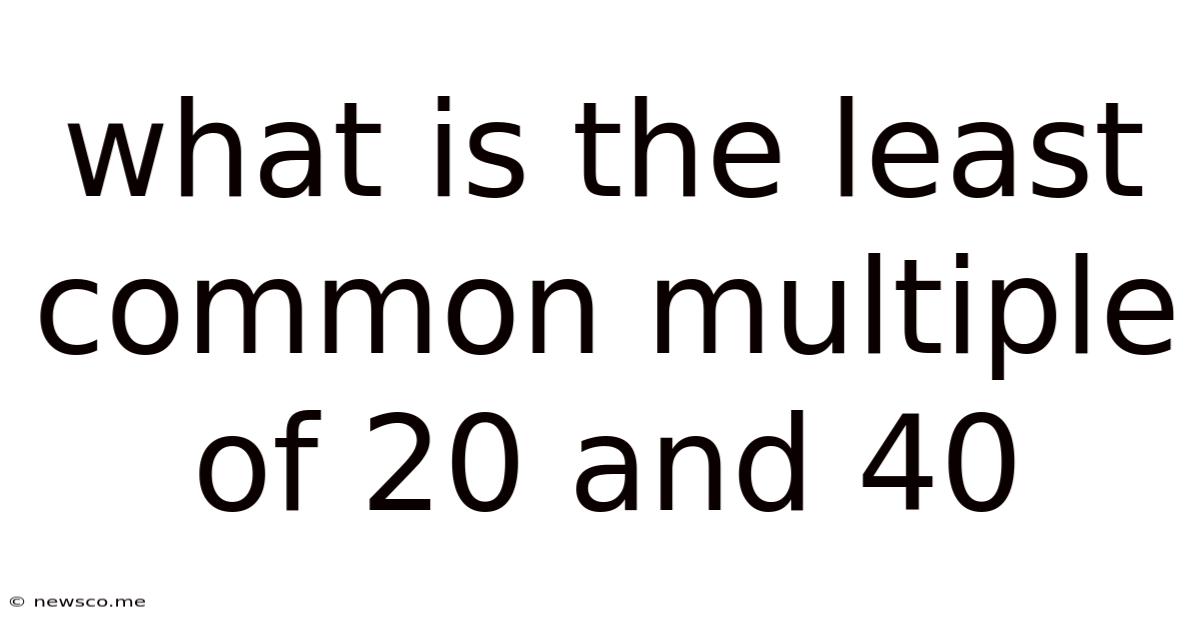
Table of Contents
What is the Least Common Multiple (LCM) of 20 and 40? A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts reveals a fascinating world of number theory with practical applications in various fields. This article delves deep into the question: What is the least common multiple of 20 and 40? We'll not only answer this question definitively but also explore different methods for calculating LCMs, their significance in mathematics, and their real-world uses.
Understanding Least Common Multiples (LCMs)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in number theory with applications ranging from simple fraction arithmetic to complex scheduling problems. Think of it as finding the smallest number that contains all the numbers you're considering as factors.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Calculating the LCM of 20 and 40: Three Methods
Now, let's tackle the specific question: What is the LCM of 20 and 40? We can employ several methods to determine this:
Method 1: Listing Multiples
The most straightforward approach is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 20: 20, 40, 60, 80, 100, 120...
- Multiples of 40: 40, 80, 120, 160...
By inspection, we see that the smallest number appearing in both lists is 40. Therefore, the LCM of 20 and 40 is 40.
Method 2: Prime Factorization
This method is more efficient for larger numbers. We first find the prime factorization of each number:
- 20 = 2² x 5
- 40 = 2³ x 5
The LCM is found by taking the highest power of each prime factor present in either factorization and multiplying them together:
LCM(20, 40) = 2³ x 5 = 8 x 5 = 40
This method is particularly useful when dealing with larger numbers where listing multiples becomes cumbersome. It provides a systematic approach to finding the LCM, regardless of the size of the numbers involved.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are intimately related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. This relationship is expressed as:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 20 and 40 using the Euclidean algorithm:
- Divide 40 by 20: 40 ÷ 20 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the divisor, which is 20.
Now, we can use the formula:
LCM(20, 40) = (20 x 40) / GCD(20, 40) = (20 x 40) / 20 = 40
This method demonstrates the interconnectedness of LCM and GCD, offering an alternative approach to calculating the LCM.
The Significance of LCM in Mathematics and Beyond
The concept of LCM extends far beyond simple arithmetic exercises. It plays a crucial role in various mathematical areas and has practical applications in real-world scenarios.
Applications in Mathematics:
- Fraction Addition and Subtraction: Finding the LCM of the denominators is essential for adding or subtracting fractions with different denominators. This allows us to express the fractions with a common denominator, simplifying the calculation.
- Modular Arithmetic: LCM is fundamental in modular arithmetic, which deals with remainders after division. It's used in cryptography and other areas of computer science.
- Number Theory: LCM is a core concept in number theory, providing insights into the relationships between integers and their factors. It's used in proving theorems and solving number-theoretic problems.
Real-World Applications:
- Scheduling: Imagine you have two machines that complete a cycle every 20 and 40 minutes respectively. To find when both machines will be at the starting point of their cycle simultaneously, you need to find the LCM of 20 and 40, which is 40 minutes.
- Gear Ratios: In mechanical engineering, LCM is used to calculate gear ratios and determine the synchronization of rotating components.
- Music Theory: The LCM is utilized in understanding musical intervals and harmonies. It helps determine when different musical notes will align perfectly.
- Project Management: In project scheduling, LCM can help determine the optimal timing for completing tasks that are interdependent.
Advanced Concepts and Extensions
The concept of LCM extends to more than two numbers. Finding the LCM of multiple numbers involves similar principles, using prime factorization or other methods to identify the smallest number divisible by all the given numbers.
Furthermore, the concept of LCM can be generalized to other algebraic structures beyond integers, such as polynomials. The techniques used to find the LCM remain analogous, adapting to the specific algebraic properties of the system involved.
Conclusion: The Power of Understanding LCMs
The seemingly simple question of finding the LCM of 20 and 40 opens the door to a rich understanding of number theory and its practical implications. By exploring different methods for calculating LCMs and understanding their significance in various fields, we appreciate their power as a fundamental mathematical tool. Whether dealing with fractions, scheduling problems, or more advanced mathematical concepts, the ability to efficiently calculate and understand LCMs is a valuable asset. From its humble beginnings in basic arithmetic to its presence in complex systems, the LCM remains a cornerstone of mathematical reasoning and practical application.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 20 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.