What Is The Least Common Multiple Of 25 And 15
News Co
Apr 05, 2025 · 5 min read
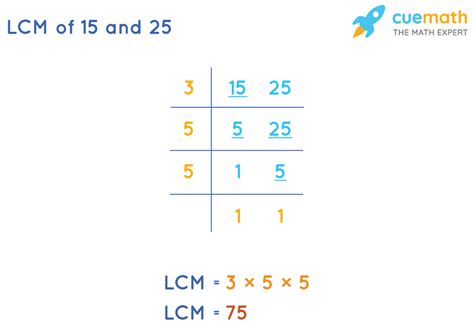
Table of Contents
What is the Least Common Multiple (LCM) of 25 and 15? A Deep Dive into Finding LCMs
Finding the least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex problems in various fields like scheduling and music theory. This article will thoroughly explore how to find the LCM of 25 and 15, providing multiple methods and explaining the underlying mathematical principles. We'll also delve into the broader context of LCMs and their significance.
Understanding Least Common Multiples
Before we tackle the specific problem of finding the LCM of 25 and 15, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers divide into evenly.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... and the multiples of 3 are 3, 6, 9, 12, 15, 18... The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is 6.
Method 1: Listing Multiples
The most straightforward method for finding the LCM, especially for smaller numbers like 25 and 15, is to list the multiples of each number until you find the smallest common multiple.
Multiples of 25: 25, 50, 75, 100, 125, 150, 175...
Multiples of 15: 15, 30, 45, 60, 75, 90, 105...
By comparing the lists, we can see that the smallest number appearing in both lists is 75. Therefore, the LCM of 25 and 15 is 75.
This method works well for smaller numbers but becomes less practical for larger numbers or when dealing with multiple numbers simultaneously.
Method 2: Prime Factorization
A more efficient and widely applicable method for finding the LCM is through prime factorization. This method involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Prime factorization of 25: 25 = 5 x 5 = 5²
Prime factorization of 15: 15 = 3 x 5
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations:
- The prime factor 3 appears once in the factorization of 15 (3¹).
- The prime factor 5 appears twice in the factorization of 25 (5²).
To find the LCM, we multiply these highest powers together: 3¹ x 5² = 3 x 25 = 75. This confirms our result from the listing method.
The prime factorization method is particularly useful for larger numbers because it provides a systematic way to find the LCM, regardless of the size of the numbers involved.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest number that divides both numbers evenly. There's a useful formula connecting the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two numbers, and |a x b| represents the absolute value of their product.
Let's find the GCD of 25 and 15 using the Euclidean algorithm:
- Divide the larger number (25) by the smaller number (15): 25 ÷ 15 = 1 with a remainder of 10.
- Replace the larger number with the smaller number (15) and the smaller number with the remainder (10): 15 ÷ 10 = 1 with a remainder of 5.
- Repeat the process: 10 ÷ 5 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 5.
Now, we can use the formula:
LCM(25, 15) = (|25 x 15|) / GCD(25, 15) = (375) / 5 = 75
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond simple mathematical exercises. It finds practical applications in various real-world scenarios:
1. Scheduling and Time Management:
Imagine you have two machines that complete a cycle in 25 minutes and 15 minutes respectively. The LCM (75 minutes) determines when both machines will complete a cycle simultaneously again. This is crucial for coordinating tasks and optimizing schedules.
2. Music Theory:
In music, the LCM is used to determine the least common denominator of rhythmic patterns and musical phrases. It ensures that different musical lines harmonize and align smoothly.
3. Construction and Engineering:
LCM is vital in various aspects of construction, from coordinating the lengths of materials to ensuring the synchronization of different parts of a complex project.
4. Computer Science:
In computer programming, the LCM can be applied in tasks involving synchronization, particularly in multi-threaded applications. It helps in coordinating the execution of different processes or threads.
5. Everyday Life:
Even in everyday tasks, understanding LCM can be beneficial. For instance, if you need to measure out ingredients in fractions of cups or spoons, the LCM can help you determine the smallest unit that accommodates all measurements.
Conclusion: Mastering the LCM
Finding the least common multiple is a fundamental skill with practical implications across numerous disciplines. While the simple listing method is suitable for smaller numbers, the prime factorization method and the GCD method provide more efficient and versatile approaches, especially when dealing with larger numbers or multiple numbers. Understanding and applying these methods not only enhances mathematical proficiency but also allows for effective problem-solving in real-world contexts. The LCM of 25 and 15, as we've comprehensively shown, is definitively 75. Remember, mastering the LCM equips you with a powerful tool for various mathematical and practical applications.
Latest Posts
Latest Posts
-
Whats The Square Root Of 256
Apr 06, 2025
-
Is 0 A Multiple Of 3
Apr 06, 2025
-
What Is The Vertical Angles Theorem
Apr 06, 2025
-
What Is The 10 Percent Of 500
Apr 06, 2025
-
What Is The Least Common Multiple Of 9 And 18
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 25 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
