What Is The Least Common Multiple Of 25 And 30
News Co
May 07, 2025 · 4 min read
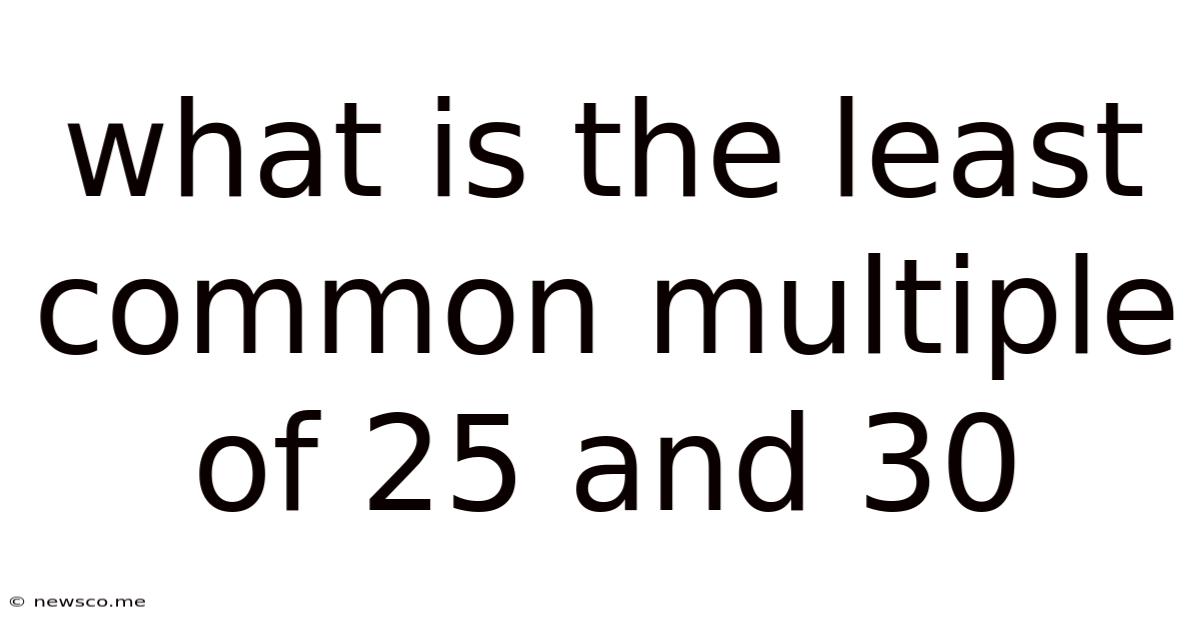
Table of Contents
What is the Least Common Multiple (LCM) of 25 and 30? A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles reveals a fascinating glimpse into number theory. This article will explore not only how to calculate the LCM of 25 and 30 but also delve into the broader concepts, methods, and applications of LCMs, providing a comprehensive understanding for students and enthusiasts alike.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors. For instance, if we consider the numbers 4 and 6, their multiples are:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32…
- Multiples of 6: 6, 12, 18, 24, 30, 36…
The common multiples of 4 and 6 are 12, 24, 36, and so on. The smallest of these common multiples is 12, therefore, the LCM(4, 6) = 12.
Calculating the LCM of 25 and 30: Three Methods
Now, let's tackle the specific problem: finding the LCM of 25 and 30. We'll explore three common methods:
Method 1: Listing Multiples
This method is straightforward but can be time-consuming for larger numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 25: 25, 50, 75, 100, 125, 150, 175, 200…
- Multiples of 30: 30, 60, 90, 120, 150, 180, 210…
The smallest common multiple is 150. Therefore, LCM(25, 30) = 150.
Method 2: Prime Factorization
This method is generally more efficient, especially for larger numbers. We find the prime factorization of each number and then construct the LCM using the highest powers of each prime factor present.
- Prime factorization of 25: 5²
- Prime factorization of 30: 2 × 3 × 5
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2¹
- Highest power of 3: 3¹
- Highest power of 5: 5²
LCM(25, 30) = 2¹ × 3¹ × 5² = 2 × 3 × 25 = 150
Method 3: Using the Greatest Common Divisor (GCD)
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) = (|a × b|) / GCD(a, b)
First, we find the GCD of 25 and 30 using the Euclidean algorithm:
- Divide 30 by 25: 30 = 25 × 1 + 5
- Divide 25 by the remainder 5: 25 = 5 × 5 + 0
The GCD is the last non-zero remainder, which is 5. Now, we apply the formula:
LCM(25, 30) = (25 × 30) / 5 = 750 / 5 = 150
Applications of LCM in Real-World Scenarios
While LCM might seem like an abstract mathematical concept, it has several practical applications:
-
Scheduling: Imagine you have two machines that operate on different cycles. One completes a cycle every 25 minutes, and the other every 30 minutes. To determine when both machines will simultaneously complete a cycle, you need to find the LCM (150 minutes).
-
Fractions: Finding the LCM is crucial when adding or subtracting fractions with different denominators. To add 1/25 and 1/30, you first find the LCM of 25 and 30 (150), then convert each fraction to an equivalent fraction with a denominator of 150 before adding them.
-
Patterning and Cycles: LCM is valuable in identifying repeating patterns or cycles in various fields like physics, engineering, and computer science. For example, understanding the LCM of different frequencies in a sound wave can be important in acoustics.
-
Project Management: In project management, the LCM can be useful in scheduling tasks that depend on multiple factors with different completion times. Determining the least common multiple of the individual task times can help determine the earliest completion time for the entire project.
Extending the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method remains particularly efficient. For example, to find the LCM of 25, 30, and 15:
-
Prime Factorization:
- 25 = 5²
- 30 = 2 × 3 × 5
- 15 = 3 × 5
-
Identify Highest Powers:
- Highest power of 2: 2¹
- Highest power of 3: 3¹
- Highest power of 5: 5²
-
Calculate LCM: LCM(25, 30, 15) = 2¹ × 3¹ × 5² = 150
Conclusion: The Importance of Understanding LCM
The least common multiple, while seemingly a basic concept, underpins numerous applications across diverse fields. Mastering the different methods for calculating the LCM, particularly the prime factorization method, provides a powerful tool for solving problems related to cycles, scheduling, fractions, and more. This understanding is not just beneficial for mathematical pursuits but also for tackling real-world challenges requiring efficient and precise calculations. The LCM of 25 and 30, as we've seen, is 150 – a seemingly simple answer that speaks volumes about the underlying elegance and power of number theory. Understanding these fundamentals provides a solid base for further exploration of advanced mathematical concepts.
Latest Posts
Latest Posts
-
Sum Of Geometric Series When R Is Less Than 1
May 08, 2025
-
Which Values Are Within The Range Of The Piecewise Defined Function
May 08, 2025
-
Set Builder Notation All Real Numbers
May 08, 2025
-
Determine If A Line Is Parallel Or Perpendicular
May 08, 2025
-
Write The Rule To Describe The Transformation
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 25 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.