What Is The Least Common Multiple Of 3 9 15
News Co
Mar 17, 2025 · 5 min read
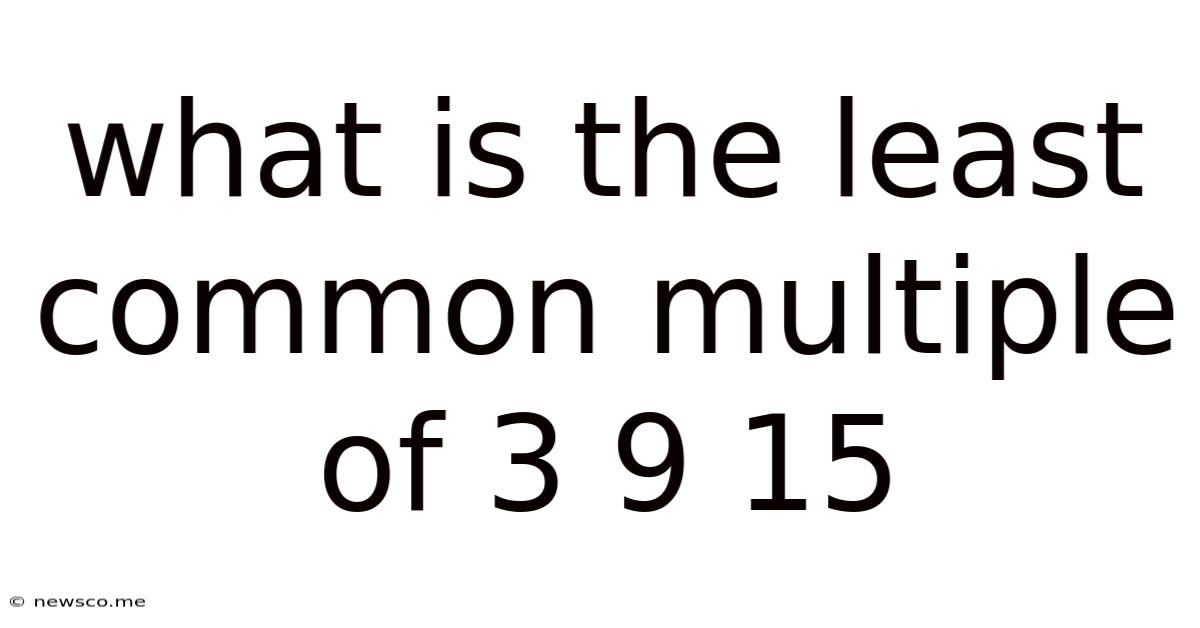
Table of Contents
What is the Least Common Multiple (LCM) of 3, 9, and 15? A Deep Dive into Finding the LCM
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for various mathematical applications, from simplifying fractions to solving complex algebraic equations. This article will delve into the process of determining the LCM of 3, 9, and 15, exploring multiple approaches and highlighting their practical applications. We’ll also touch upon the broader significance of LCM in mathematics and beyond.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 3, 9, and 15, let's establish a firm understanding of what the LCM actually is. The least common multiple is the smallest positive integer that is a multiple of all the integers in a given set. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12… and the multiples of 3 are 3, 6, 9, 12, 15… The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
This concept is fundamental in various mathematical operations, including:
- Simplifying fractions: Finding the LCM of the denominators allows you to add or subtract fractions with different denominators easily.
- Solving equations: LCM plays a crucial role in solving equations involving fractions and rational expressions.
- Real-world applications: LCM finds applications in scheduling problems, determining cycles in repeating events, and even in music theory.
Methods for Finding the LCM of 3, 9, and 15
Now, let's focus on finding the LCM of 3, 9, and 15. We'll explore several methods to achieve this:
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45...
- Multiples of 9: 9, 18, 27, 36, 45, 54...
- Multiples of 15: 15, 30, 45, 60...
By comparing the lists, we can see that the smallest multiple common to all three numbers is 45. Therefore, the LCM of 3, 9, and 15 is 45.
This method is effective for smaller numbers but becomes cumbersome and time-consuming when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
-
Prime factorization:
- 3 = 3¹
- 9 = 3²
- 15 = 3¹ x 5¹
-
Constructing the LCM: We take the highest power of each prime factor present in the factorizations:
- Highest power of 3: 3² = 9
- Highest power of 5: 5¹ = 5
-
Multiplying the highest powers: Multiply the highest powers together: 9 x 5 = 45
Therefore, the LCM of 3, 9, and 15 is 45. This method is more systematic and efficient, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers. While finding the GCD first might seem like an extra step, it can simplify calculations, especially with larger numbers. Let's use this method for our example:
-
Find the GCD of 3, 9, and 15: The greatest common divisor of these three numbers is 3.
-
Use the formula (modified for three numbers): This formula doesn't directly extend to three numbers in a straightforward manner. However, we can use the pairwise approach. First, find the LCM of 3 and 9 using prime factorization: This is 9. Then, find the LCM of 9 and 15 using prime factorization: This is 45.
-
Result: The LCM of 3, 9, and 15 is 45.
While this method might seem more complex for this specific example, its efficiency becomes more apparent when dealing with larger numbers where finding the GCD becomes a powerful tool.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond the realm of abstract mathematics. It finds practical applications in numerous real-world scenarios:
-
Scheduling: Imagine two buses depart from the same station, one every 3 minutes and the other every 9 minutes. The LCM (9) determines when both buses will depart simultaneously again.
-
Calendars and events: Recurring events, like the alignment of planets or the timing of festivals, often involve periods that are multiples of different numbers. Finding the LCM helps predict when these events will coincide.
-
Manufacturing and production: In factory settings, machines might operate on different cycles. Understanding the LCM of their cycle times is crucial for optimizing production schedules and minimizing downtime.
-
Music: The frequency of musical notes and the creation of harmonies often involve multiples of fundamental frequencies. The LCM plays a role in understanding consonance and dissonance.
-
Construction: Matching different building materials and their dimensions often involves finding the LCM to ensure efficient and aesthetically pleasing designs.
Conclusion: Mastering LCM for Mathematical Proficiency and Beyond
Understanding and effectively calculating the least common multiple is a fundamental skill in mathematics with wide-ranging applications. Whether you're simplifying fractions, solving equations, or tackling real-world problems involving cyclical events, the ability to find the LCM is essential. This article explored various methods for calculating the LCM, highlighting the efficiency of prime factorization, and demonstrating the power of connecting LCM with the GCD. Mastering these concepts not only strengthens your mathematical abilities but also equips you to solve problems in diverse fields, contributing to your overall analytical and problem-solving skills. The LCM of 3, 9, and 15, as we have demonstrated through multiple methods, is undeniably 45, solidifying the understanding of this fundamental mathematical principle. Remember to choose the method best suited to the numbers you are working with – listing multiples works well for smaller numbers, while prime factorization proves more efficient for larger and more complex calculations.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 3 9 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.