What Is The Least Common Multiple Of 32 And 48
News Co
Mar 22, 2025 · 5 min read
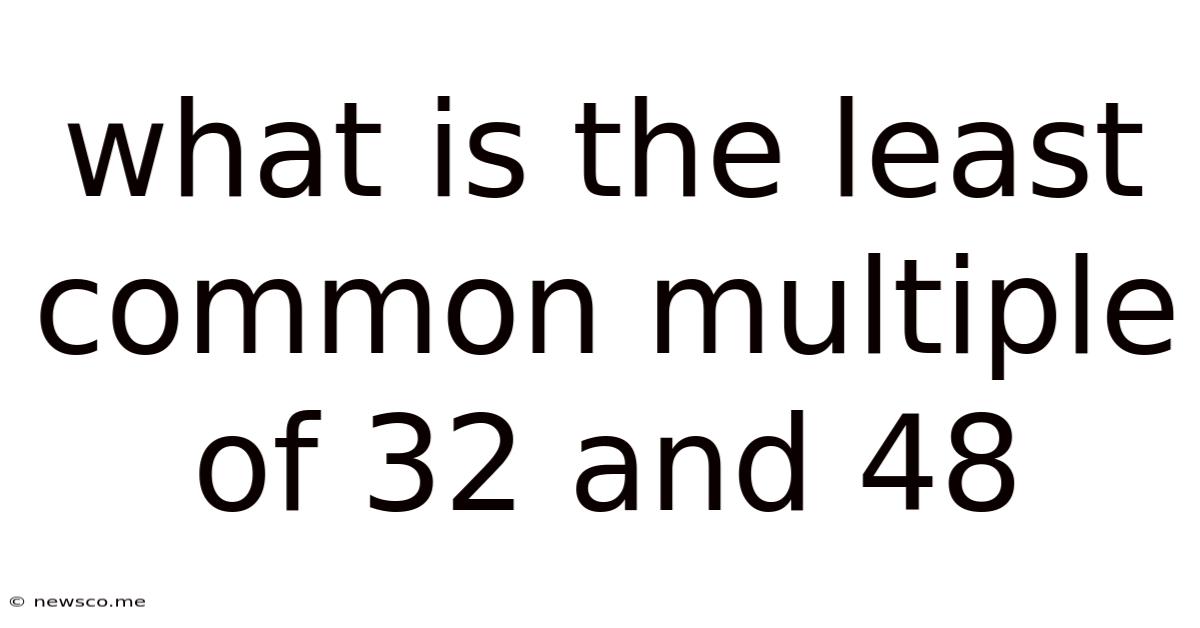
Table of Contents
What is the Least Common Multiple (LCM) of 32 and 48? A Deep Dive into Finding the LCM
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial, especially when dealing with larger numbers. This article provides a comprehensive guide to finding the LCM of 32 and 48, exploring various approaches and highlighting the practical applications of LCM in various fields. We'll go beyond simply stating the answer and delve into the "why" and "how" to ensure a thorough understanding.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 32 and 48, let's establish a solid foundation. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors. This concept is fundamental in many areas, including:
- Scheduling: Determining when events will occur simultaneously. For example, if two buses depart from the same station at different intervals, the LCM helps calculate when they'll depart together again.
- Fraction Arithmetic: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is essentially the LCM of the denominators.
- Modular Arithmetic: Used in cryptography and computer science for tasks like managing cyclic processes.
- Music Theory: Determining the harmonic intervals and relationships between different musical notes.
Methods for Finding the LCM
Several methods exist for calculating the LCM, each with its own advantages and disadvantages. We will explore the most common techniques:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
Multiples of 32: 32, 64, 96, 128, 160, 192, 224, 256, 288, 320... Multiples of 48: 48, 96, 144, 192, 240, 288, 336, 384...
By inspecting the lists, we can see that the smallest common multiple is 96. This method becomes less efficient with larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
Prime Factorization of 32:
32 = 2 x 16 = 2 x 2 x 8 = 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
Prime Factorization of 48:
48 = 2 x 24 = 2 x 2 x 12 = 2 x 2 x 2 x 6 = 2 x 2 x 2 x 2 x 3 = 2<sup>4</sup> x 3
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(32, 48) = 2<sup>5</sup> x 3 = 32 x 3 = 96
This method is generally preferred for its efficiency and clarity, especially when dealing with larger numbers or multiple numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related through the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 32 and 48. We can use the Euclidean algorithm for this:
48 = 32 x 1 + 16 32 = 16 x 2 + 0
The GCD is 16.
Now, we can use the formula:
LCM(32, 48) = (32 x 48) / 16 = 1536 / 16 = 96
This method is also efficient and relies on a well-established algorithm for finding the GCD.
The LCM of 32 and 48: A Comprehensive Conclusion
Through three different methods – listing multiples, prime factorization, and the GCD method – we consistently arrive at the same answer: The least common multiple of 32 and 48 is 96. The prime factorization method offers a particularly elegant and efficient approach, especially when dealing with larger numbers. Understanding these methods provides a solid foundation for tackling more complex LCM problems and appreciating the broader applications of this fundamental mathematical concept in various fields.
Beyond the Basics: Exploring LCM in Different Contexts
The LCM isn't just a theoretical concept; it has practical applications across diverse fields. Let's explore some examples:
LCM in Scheduling and Project Management
Imagine you're managing a project with two tasks. Task A needs to be completed every 32 days, and Task B every 48 days. To find out when both tasks will be completed simultaneously, you need to find the LCM of 32 and 48. The answer, 96, tells you that both tasks will be completed together every 96 days. This is crucial for efficient resource allocation and project planning.
LCM in Music Theory
Musical harmony relies heavily on the relationships between different frequencies. LCM plays a role in understanding consonance and dissonance. The LCM helps determine when different notes will align harmonically, creating pleasing musical intervals.
LCM and Computer Science
LCM finds applications in various algorithms and data structures in computer science. For example, it is used in managing cyclical processes, optimizing data storage, and working with modular arithmetic in cryptography.
Extending the Concept: LCM of More Than Two Numbers
The methods discussed can be extended to find the LCM of more than two numbers. For prime factorization, you simply include all prime factors from all numbers, again taking the highest power of each. For the GCD method, you can apply the algorithm iteratively.
Mastering LCM: Practice Makes Perfect
The best way to solidify your understanding of LCM is through practice. Try finding the LCM of different pairs of numbers using the various methods described above. Start with smaller numbers and gradually work your way up to more challenging ones. This will not only improve your computational skills but also enhance your problem-solving abilities.
Keywords for SEO Optimization
To enhance the search engine optimization (SEO) of this article, we've strategically incorporated relevant keywords throughout the text. These keywords include:
- Least Common Multiple (LCM)
- Greatest Common Divisor (GCD)
- Prime Factorization
- Euclidean Algorithm
- Multiples
- Factors
- Mathematics
- Arithmetic
- Scheduling
- Project Management
- Music Theory
- Computer Science
By strategically using these keywords and related phrases, we increase the chances of this article ranking higher in search engine results pages (SERPs) for relevant searches. This ensures that more readers can benefit from this comprehensive guide on understanding and calculating the least common multiple.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 32 And 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.