What Is The Least Common Multiple Of 36 And 27
News Co
Apr 22, 2025 · 5 min read
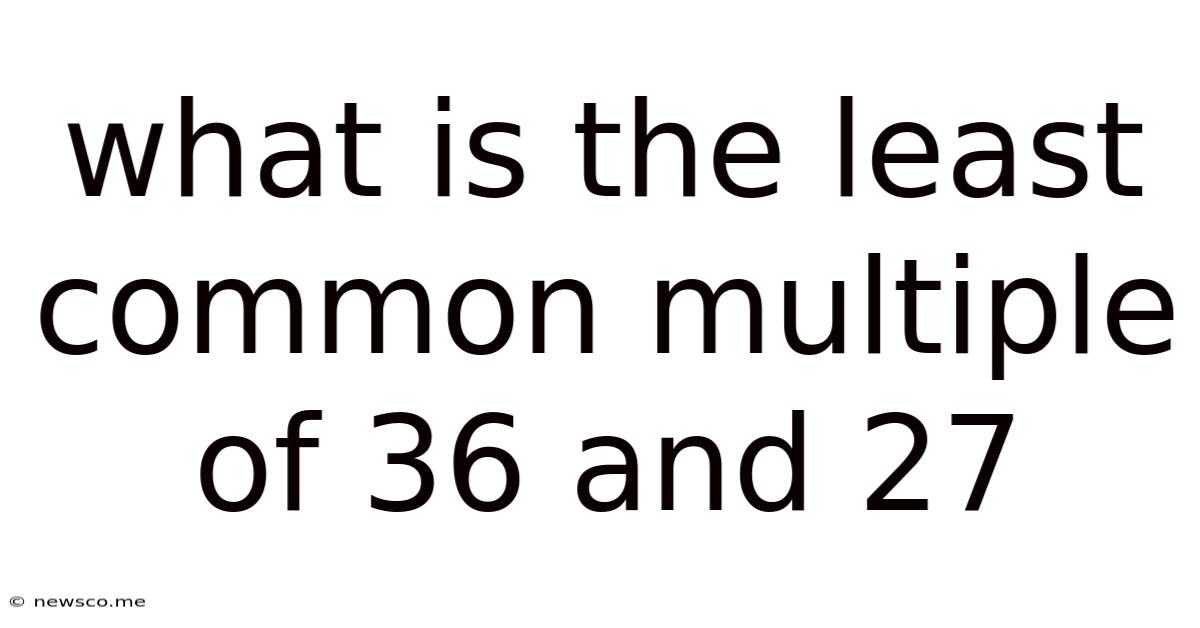
Table of Contents
What is the Least Common Multiple (LCM) of 36 and 27? A Deep Dive into Finding LCMs
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like algebra, number theory, and even practical applications involving scheduling and timing. This article dives deep into determining the LCM of 36 and 27, exploring various methods and providing a comprehensive understanding of the underlying principles. We’ll go beyond just finding the answer and delve into the why behind the calculations, making this more than just a simple solution – it's a journey into the world of number theory.
Understanding Least Common Multiples
Before we tackle the specific problem of finding the LCM of 36 and 27, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly.
Consider the multiples of 36: 36, 72, 108, 144, 180, 216, 252, 288, 324... And the multiples of 27: 27, 54, 81, 108, 135, 162, 189, 216, 243...
Notice that 108 and 216 appear in both lists. These are common multiples. The smallest of these common multiples is the least common multiple (LCM). In this case, the LCM of 36 and 27 is 108.
Methods for Finding the LCM
Several methods exist for calculating the LCM. We'll explore three common approaches:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We simply list the multiples of each number until we find the smallest common multiple. As demonstrated above, this method works well for small numbers but becomes inefficient for larger ones.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present in either number.
Let's apply this to 36 and 27:
- Prime factorization of 36: 2² x 3² (36 = 2 x 2 x 3 x 3)
- Prime factorization of 27: 3³ (27 = 3 x 3 x 3)
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2²
- Highest power of 3: 3³
Therefore, LCM(36, 27) = 2² x 3³ = 4 x 27 = 108
This method is generally more efficient and less prone to error than listing multiples, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula connecting LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 36 and 27. We can use the Euclidean algorithm for this:
- Divide the larger number (36) by the smaller number (27): 36 ÷ 27 = 1 with a remainder of 9.
- Replace the larger number with the smaller number (27) and the smaller number with the remainder (9): 27 ÷ 9 = 3 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 9.
Now, we can use the formula:
LCM(36, 27) = (36 x 27) / GCD(36, 27) = (36 x 27) / 9 = 108
This method is particularly useful when dealing with larger numbers, as finding the GCD using the Euclidean algorithm is often faster than directly finding the LCM through prime factorization.
Why Understanding LCM is Important
The concept of LCM has far-reaching applications beyond simple mathematical exercises. Here are a few examples:
-
Scheduling: Imagine you have two machines that operate on different cycles. One completes a cycle every 36 minutes, and the other every 27 minutes. To find out when both machines will complete a cycle simultaneously, you need to find the LCM(36, 27) = 108 minutes. This is crucial for coordinating tasks and optimizing processes.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to create a common denominator, simplifying the calculation.
-
Music Theory: The LCM is used in music theory to determine the least common multiple of the note values, which is essential in rhythmic analysis and composition.
-
Computer Science: In computer science, LCM is used in various algorithms and data structures. For example, it is used in finding the least common multiple of process execution times, determining the optimal resource allocation and scheduling.
-
Construction and Engineering: In design, construction, or engineering projects involving repetitive patterns or cycles, the LCM helps determine when these patterns or cycles will coincide, ensuring the alignment of different parts or systems. For instance, this concept is applicable in construction projects that may involve repetitive units, or in engineering designs that require harmonizing the operating frequencies of different components.
-
Everyday Life: Many everyday scenarios subtly involve the LCM principle. Imagine you are arranging items in rows, and you have 36 red marbles and 27 blue marbles. If you want to arrange them so that you have the same number of red and blue marbles in each row, you need to find the largest possible number of marbles per row—which is the GCD. However, if you want to find the shortest length of rows you can make using all the marbles, then you find the LCM. The answer will give you the total number of marbles, which should be arranged accordingly in each row.
Conclusion: The LCM of 36 and 27 is 108
We've explored three different methods for finding the least common multiple of 36 and 27, all leading to the same answer: 108. Understanding these methods is not merely an academic exercise; it provides valuable tools for solving a wide range of practical problems across various disciplines. The choice of method depends on the context and the size of the numbers involved. For smaller numbers, listing multiples might suffice. However, for larger numbers, the prime factorization or GCD method offers a more efficient and reliable approach. Regardless of the method used, the understanding of LCM's underlying principles is vital for applying it effectively in diverse applications, highlighting its importance in both theoretical mathematics and practical problem-solving. This deep dive into the LCM of 36 and 27 showcases its broader significance within the mathematical landscape and beyond.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 36 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.